Dãy nào sau đây có giới hạn khác 0?
A. 3 n + 2 2 n
B. 1 2 n
C. cos 3 n 2 n
D. 1 n 2
Dãy số nào sau đây có giới hạn khác 0 ?
A. - 0 , 9 n
B. n - 3 n
C. 2 n - 1 3 n + 2 n
D. 1 - n n 2 - 1
Từ lim n → + ∞ q n = 0 ; q < 1 có lim − 0 , 9 n = 0
lim n − 3 n = lim 1 − 3 n 1 = 1
2 n − 1 3 n + 2 n = 2 3 n − 1 3 n 1 + 2 3 n có lim 2 n − 1 3 n + 2 n = lim 2 3 n − 1 3 n 1 + 2 3 n = 0
lim 1 − n n 2 − 1 = lim 1 n 2 − 1 n 1 − 1 n 2 = 0
Chọn đáp án B.
Dãy số nào sau đây có giới hạn khác 0?
A. 1/n
B. 1 / n
C. (n+1)/n
D. ( sin n ) / n
- Cách 1:
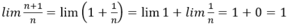
Đáp án C
- Cách 2 (phương pháp loại trừ): Từ các định lí ta thấy:
Các dãy ở phương án A,B đều bằng 0, do đó loại phương án A,B
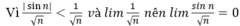
Do đó loại phương án D. Chọn đáp án C
Dãy số nào sau đây có giới hạn khác 0?
A. 1 n
B. n + 1 n
C. sin n n
D. 1 n
Trong các dãy số sau, dãy số nào có giới hạn khác 0 ?
A. u n = 0,1234 n
B. u n = − 1 n n
C. u n = 4 n 3 − n + 1 n n + 3 + 1
D. u n = cos2n n
Đáp án C
Mẹo nhanh: trên tử và mẫu của cau C ta loại trừ đi các đa thức bậc thấp hơn đi và để lại đa thức bậc cao nhất.
l i m 4 n 3 − n + 1 n n + 3 + 1 = lim 4 n 3 n n = 2.
Trong các dãy số sau, dãy số nào có giới hạn khác 0 ?
A. u n = 2 n − 1 n
B. u n = 1 n n + 1
C. u n = 1 3 n
D. u n = 1 n 2 + 1
Đáp án A
Ta có:
lim 2 n − 1 n = lim 2 − 1 n = 2 ≠ 0 ; lim 1 n n + 1 = 0 ; lim 1 3 n = 0 ; lim 1 n 2 + 1 = 0.
Vậy chỉ có dãy số u n = 2 n − 1 n có giới hạn khác 0.
Dãy nào sau đây có giới hạn bằng 0?
A. - 5 4 n
B. - 4 π n
C. π 4 n
D. - 4 3 n
Dãy số nào sau đây có giới hạn bằng 0?
A. u n = n 2 - 2 n 5 n + 5 n 2
B. u n = 1 - 2 n 5 n + 5
C. u n = 1 - 2 n 2 5 n + 5
D. u n = 1 - 2 n 5 n + 5 n 2
Dãy số nào sau đây có giới hạn bằng 0?
A. ( 0 , 81 ) n
B. ( - 1 , 15 ) n
C. ( 1 , 016 ) n
D. ( - 1 , 94 ) n
Dãy số nào sau đây có giới hạn bằng 0?
A. l i m n 2 - 2 n 5 n + 5 n 2
B. l i m 1 - 2 n 5 n + 5
C. l i m 1 - 2 n 2 5 n + 5
D. l i m 1 - 2 n 5 n + 5 n 2
Ta có lim 1 − 2 n 5 n + 5 n 2 = lim n 2 1 n 2 − 2 n n 2 5 n + 5 = lim 1 n 2 − 2 n 5 n + 5 = 0 5 = 0 .
Chọn đáp án D