Cho hình lập phương ABCD.A’B’C’D’ có các cạnh bằng 1. M là trung điểm CC’. Tính góc giữa hai đường thẳng AD’ và BM.
A. 18 0 26 '
B. 45 0
C. 26 0 33 '
D. 18 0 43 '
Cho hình lập phương A B C D . A ' B ' C ' D ' có các cạnh bằng 1. M là trung điểm CC'. Tính góc giữa hai đường thẳng AD' và BM.
A. 45 °
B. 18 ° 26 '
C. 26 ° 33 '
D. 18 ° 43 '
Cho hình lập phương ABCD.A'B'C'D' có các cạnh bằng 1. M là trung điểm CC'. Tính góc giữa hai đường thẳng AD' và BM
A. 45 o
B. 18 o 26 '
C. 26 o 33 '
D. 18 o 43 '
Cho hình lập phương ABCD.A’B’C’D’. Gọi M,N,P lần lượt là trung điểm của các cạnh AB, AD, C’D’. Tính cosin góc giữa hai đường thẳng MN và CP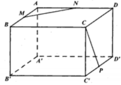
![]()
![]()
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Các điểm M, N, P lần lượt thuộc các đường thẳng AA’,BB’,CC’ thỏa mãn diện tích của tam giác MNP bằng a 2 . Góc giữa hai mặt phẳng (MNP) và (ABCD) là
A. 60 o
B. 30 o
C. 45 o
D. 120 o
Cho hình lập phương ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của AA’ và CD. Góc giữa hai đường thẳng BM và C’N bằng:
A. 45 0
B. 30 0
C. 60 0
D. 90 0
Đáp án D
Gọi E là trung điểm A’B’. Khi đó ANC’E là hình bình hành. Suy ra C’N song song với AE. Như vậy góc giữa hai đường thẳng BM và C’N bằng góc giữa hai đường thẳng BM và AE. Ta có Δ M A B = Δ E A ’ A c − g − c suy ra A ' A E ^ = A B M ^ (hai góc tương ứng).
Do đó: A ' A E ^ + B M A ^ = A B M ^ + B M A ^ = 90 0 . Suy ra hai đường thẳng BM và AE vuông góc với nhau nên góc gữa chúng bằng 90 0 . Vậy góc giữa hai đường thẳng BM và C’N bằng 90 0 .
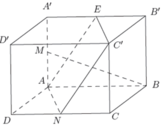
Cho hình lập phương ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của AA’ và CD. Góc giữa hai đường thẳng BM và C’N bằng:
A. 45 0
B. 30 0
C. 60 0
D. 90 0
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi M là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng AM và DB’
A. a 2 7
B. a 4
C. 2 7 a
D. a 2
Đáp án A
Phương pháp:
- Sử dụng phương pháp tọa độ hóa.
- Công thức tính khoảng cách giữa hai đường thẳng chéo nhau:
Cho ∆ có VTCP u → và qua M; ∆ ' có VTCP v → và qua M’

Cách giải:
Gắn hệ trục tọa độ như hình vẽ, trong đó:
A'(0;0;0), B'(0;a;0), C'(a;a;0), D'(a;0;0)
A(0;0;a), B(0;a;a), C(a;a;a); D(a;0;a), M(a/2;a;a)
Đường thẳng AM có VTCP ![]() và qua A(0;0;a)
và qua A(0;0;a)
Đường thẳng DB’ có VTCP ![]() và qua D(a;0;a)
và qua D(a;0;a)
A D → = ( a ; 0 ; 0 )
Khoảng cách giữa hai đường thẳng AM và DB’: 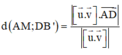
Ta có:
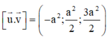
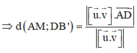

Vây, khoảng cách giữa AM và DB’ là a 2 7
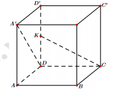
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi K là trung điểm của DD¢. Khoảng cách giữa hai đường thẳng chéo nhau CK và AD¢ bằng:
A. a 3 3
B. a 3 2
C. 2 a 3 3
D. a 3
Đáp án D
Chọn hệ trục với D 0 ; 0 ; 0 , A a ; 0 ; 0 , A ' a ; 0 ; a , K 0 ; 0 ; a 2 , C 0 ; a ; 0
Khi đó D A ' → = a ; 0 ; a , K C → 0 ; a ; - a 2 ⇒ D A ' → ; K C → = a 2 2 2 ; - 1 ; - 2
Phương trình mặt phẳng qua C (chứa CK) và song song với DA’ là (P):2x - y - 2z + a = 0
Khi đó d C K ; A ' D = d D ; P = a 3 .
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Gọi M, N lần lượt là trung điểm của AB và CD. Tính khoảng cách giữa hai đường thẳng A’C và MN.
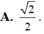
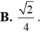
![]()
![]()