Cho tam giác ABC có A(4; – 2) , B(3; 3) , C(1; 4) .
Tứ giác OABC hình gì ? Chứng minh

Những câu hỏi liên quan
Mình cần gấp ạ....
1)Cho tam giác ABC cân tại A có AB=6 cm,BC=4 cm.Tính các góc trong tam giác ABC.
2)Cho tam giác ABC vuông tại A có góc B=50 độ,BC=5 cm.Ở phía ngoài tam giác ABC,vẽ tam giác vuông ADC có góc CAD=35 độ.Tính chu vi tam giác ABC và chu vi tam giác ADC
Câu 1:
1) Cho tam giác ABC có góc A = góc C-10độ; góc B=góc C + 10độ. Tính các góc của tam giác ABC?
2) Cho tam giác ABC có góc B= 7/6 góc C; góc A= 5/6 góc C. Tính các góc của tam giác ABC?
3) cho tam giác ABC có góc A= 2. Góc B ; góc B = góc C . tính các góc của tam giác ABC?
4) Cho tam giác ABC có góc A= 5.góc C; góc B= 2.góc C. tínhcác góc của tam giác ABC?
Bài 2 : Cho tam giác ABC có AB3cm; AC 4cm; BC 5cm . So sánh các góc của tam giác ABCBài 3 :Cho tam giác ABC có góc B60 độ ; góc C 40 độ . So sánh các cạnh của tam giác ABCBài 4 : Cho tam giác ABC có AB5cm ; AC 12 cm ; BC13 cma) Tam giác ABC là tam giác gì ?b) So sánh các góc của tam giác ABCBài 5 : Cho tam giác ABC vuông tại A có AB10cm ; AC 24 cma) Tính độ dài cạnh BC?b) Tam giác ABC là tam giác gì ?
Đọc tiếp
Bài 2 : Cho tam giác ABC có AB=3cm; AC= 4cm; BC= 5cm . So sánh các góc của tam giác ABC
Bài 3 :Cho tam giác ABC có góc B=60 độ ; góc C = 40 độ . So sánh các cạnh của tam giác ABC
Bài 4 : Cho tam giác ABC có AB=5cm ; AC= 12 cm ; BC=13 cm
a) Tam giác ABC là tam giác gì ?
b) So sánh các góc của tam giác ABC
Bài 5 : Cho tam giác ABC vuông tại A có AB=10cm ; AC= 24 cm
a) Tính độ dài cạnh BC=?
b) Tam giác ABC là tam giác gì ?
bài 2:
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
bài 2:
ta có: AB <AC <BC (Vì 3cm <4cm <5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
HT mik làm giống bạn Dương Mạnh Quyết
Đúng 0
Bình luận (0)
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC có A(3;1) B(2,6) C(4;-1) a.Tính chứ vi tam giác ABC B.Tính góc A C.Tìm toạ độ trực tâm H của tam giác ABC.
a: A(3;1); B(2;6); C(4;-1)
\(AB=\sqrt{\left(2-3\right)^2+\left(6-1\right)^2}=\sqrt{5^2+1^2}=\sqrt{26}\)
\(AC=\sqrt{\left(4-3\right)^2+\left(-1-1\right)^2}=\sqrt{2^2+1^2}=\sqrt{5}\)
\(BC=\sqrt{\left(4-2\right)^2+\left(-1-6\right)^2}=\sqrt{2^2+7^2}=\sqrt{53}\)
Chu vi tam giác ABC là:
\(C_{ABC}=\sqrt{26}+\sqrt{5}+\sqrt{53}\left(đvđd\right)\)
b: Xét ΔABC có
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{26+5-53}{2\cdot\sqrt{26\cdot5}}\simeq-0,96\)
=>\(\widehat{A}\simeq165^0\)
c: Gọi H(x,y) là trực tâm của ΔABC
\(\overrightarrow{AH}=\left(x-3;y-1\right)\)
\(\overrightarrow{BH}=\left(x-2;y-6\right)\)
\(\overrightarrow{BC}=\left(2;-7\right);\overrightarrow{AC}=\left(1;-2\right)\)
H là trực tâm nên ta có: AH\(\perp\)BC và BH\(\perp\)AC
=>\(\left\{{}\begin{matrix}\overrightarrow{AH}\cdot\overrightarrow{BC}=0\\\overrightarrow{BH}\cdot\overrightarrow{AC}=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2\left(x-3\right)+\left(-7\right)\left(y-1\right)=0\\1\left(x-2\right)+\left(-2\right)\left(y-6\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-6-7y+7=0\\x-2-2y+12=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-7y=-1\\x-2y=-10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-7y=-1\\2x-4y=-20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3y=-1+20=19\\x-2y=-10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-\dfrac{19}{3}\\x=-10+2y=-10-\dfrac{38}{3}=-\dfrac{68}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có ABC có A(2; 2; 1), B(4; 4; 2), C(-2; 4; -3). Vectơ nào dưới đây là vectơ chỉ phương của đường phân giác trong AD của tam giác ABC. A.
-
2
;
4
;
-
3
B.
6
;
0
;
5
C....
Đọc tiếp
Cho tam giác ABC có ABC có A(2; 2; 1), B(4; 4; 2), C(-2; 4; -3). Vectơ nào dưới đây là vectơ chỉ phương của đường phân giác trong AD của tam giác ABC.
A. - 2 ; 4 ; - 3
B. 6 ; 0 ; 5
C. 0 ; 1 ; - 1 3
D. - 4 3 ; - 1 3 ; - 1
Đáp án C
Ta có: ![]()
Từ điểm D kẻ đường thẳng song song với AC, cắt cạnh AB tại điểm E. Từ D kẻ đường thẳng song song với AB cắt cạnh AC tại F. Do AD là đường phân giác trong của tam giác ABC nên ta suy ra AEDF là hình thoi.
Đặt AE=AF=k. Ta có:
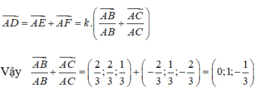
là một vectơ chỉ phương của đường thẳng AD. Từ đó suy ra C là khẳng định đúng.
Ta cũng lưu ý rằng khẳng định A sai, do tam giác ABC không cân tại đỉnh A.
Đúng 0
Bình luận (0)
Câu 1 : Cho tam giác ABC có a=3, b=4, c=7 . Tính R
Câu 2 : Cho tam giác ABC có AB=4, BC=6, CA=9 . Tính ma + hb
Câu 1:
Chú ý độ dài 3 cạnh của tam giác là sai thì \(a+b=7=c\)
Nếu là cạnh của tam giác thì: \(\left\{{}\begin{matrix}a+b>c\\a+c>b\\c+b>a\end{matrix}\right.\)
Câu 2: Ta có:
\(m_a=\sqrt{\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}}=\sqrt{\dfrac{AC^2+AB^2}{2}-\dfrac{BC^2}{4}}\)
\(\Rightarrow m_a=\sqrt{\dfrac{9^2+4^2}{2}-\dfrac{6^2}{4}}\)
\(\Rightarrow m_a\approx6,3\)
Ta có: \(p=\dfrac{AB+AC+BC}{2}=\dfrac{4+6+9}{2}=\dfrac{19}{2}\)
\(\Rightarrow S_{ABC}=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{\dfrac{19}{2}\cdot\left(\dfrac{19}{2}-6\right)\cdot\left(\dfrac{19}{2}-9\right)\cdot\left(\dfrac{19}{2}-4\right)}\approx9,5\)
\(\Rightarrow h_b=2\cdot\dfrac{S_{ABC}}{b}\Rightarrow h_b=2\cdot\dfrac{9,5}{9}\approx2,1\)
Đúng 1
Bình luận (1)
Cho tam giác ABC có a = 3 cm, b = 4 cm, c = 5 cm. Tam giác ABC là
A. Tam giác nhọn
B. Tam giác tù
C. Tam giác vuông
D. Tam giác đều
Ta có: a2 + b2 = c2 nên tam giác ABC là tam giác vuông.
Chọn C
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 4, AC = 6, A =30°. Diện tích của tam giác ABC là
A.12
B. 6
C. 6 3
D. 6 2
Diện tích tam giác ABC là:
S = 1 2 A B . A C . sin A = 1 2 .4.6. sin 30 0 = 6
ĐÁP ÁN B
Đúng 0
Bình luận (0)
Cho tam giác ABC có các cạnh thoả mãn a^4=b^4+c^4. a) Chứng minh rằng tam giác ABC có các góc đều nhọn b) Chứng minh 2sin^2A=tanB.tanC
Xem chi tiết
1 ) Cho tam giác ABC có góc A nhọn , AB=4 , AC=5 và diện tích tam giác ABC =8 . Tính BC
2 ) Cho tam giác ABC có AB=3 , góc ACB = 45° , góc ABC = 60° . Tính BC
em mới học lớp 7 hà
năm nay lên lớp 8 =)))))
Đúng 0
Bình luận (0)
1)Ta có: \(S_{ABC}=\dfrac{1}{2}AB.AC.\sin A\)
\(\Leftrightarrow8=\dfrac{1}{2}\times4\times5\times sinA\)
\(\Leftrightarrow\sin A=0,8\)
Lại có: \(\left(\sin A\right)^2+\left(\cos A\right)^2=1\Leftrightarrow\cos A=0,6.\)
Áp dụng định lí hàm số cosin:
\(BC^2=AB^2+AC^2-2AB\times AC\times\cos A\)
\(\Leftrightarrow BC^2=4^2+5^2-2\times4\times5\times0,6=17\)
\(\Leftrightarrow BC=\sqrt{17}.\)
2) Trong \(\Delta ABC\) có: \(g\text{ó}cA+g\text{óc}B+g\text{óc}C=180^o\)
=> BAC=75o.
Áp dụng định lí hàm số sin:
\(\dfrac{AB}{\sin C}=\dfrac{BC}{\sin A}\Leftrightarrow\dfrac{3}{\sin45^o}=\dfrac{BC}{\sin75^o}\)
\(\Leftrightarrow BC=\dfrac{3+3\sqrt{3}}{2}\).
Đúng 0
Bình luận (0)




















