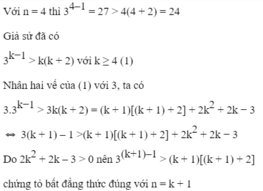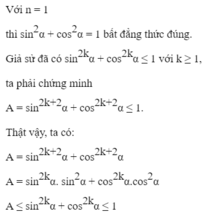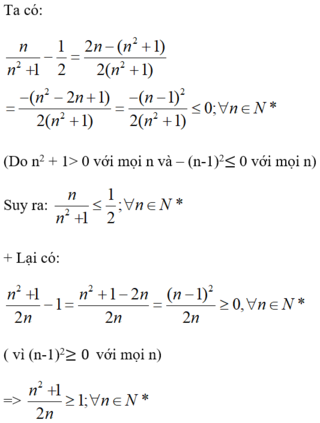Chứng minh các bất đẳng thức sau ( n ∈ N ∗ ) 2 n + 2 > 2 n + 5

Những câu hỏi liên quan
Chứng minh các bất đẳng thức sau 3n − 1 > n(n + 2) với n ≥ 4
Chứng minh các bất đẳng thức sau ( n ∈ N ∗ ) sin 2 n α + cos 2 n α ≤ 1 .
Chứng minh bất đẳng thức sau biết a;b;m;n là các số nguyên: a ^ (m + n) + b ^ (m + n) >= a ^ m * b ^ n + a ^ n * b ^ m
Chứng minh các bất đẳng thức
n
n
2
+
1
≤
1
2
và
n
2
+
1
2
n...
Đọc tiếp
Chứng minh các bất đẳng thức n n 2 + 1 ≤ 1 2 và n 2 + 1 2 n ≥ 1 với mọi n ∈ N * .
Chứng minh rằng với mọi số tự nhiên n ≥ 2 , ta có các bất đẳng thức: 2 n + 1 > 2 n + 3
2n + 1 > 2n + 3 (2)
+ Với n = 2 thì (2) ⇔ 8 > 7 (luôn đúng).
+ Giả sử (2) đúng khi n = k ≥ 2, nghĩa là 2k+1 > 2k + 3.
Ta chứng minh đúng với n= k+ 1 tức là chứng minh: 2k+2 > 2(k+ 1)+ 3
Thật vậy, ta có:
2k + 2 = 2.2k + 1
> 2.(2k + 3) = 4k + 6 = 2k + 2 + 2k + 4.
> 2k + 2 + 3 = 2.(k + 1) + 3 ( Vì 2k + 4 >3 với mọi k ≥ 2)
⇒ (2) đúng với n = k + 1.
Vậy 2n + 1 > 2n + 3 với mọi n ≥ 2.
Đúng 0
Bình luận (0)
với n>0 chứng minh bất đẳng thức sau
\(\frac{1}{2\sqrt{n+1}}< \sqrt{n+1}-\sqrt{n}< \frac{1}{2\sqrt{n}}\)
\(\frac{1}{2\sqrt{n+1}}=\frac{1}{\sqrt{n+1}+\sqrt{n+1}}< \frac{1}{\sqrt{n+1}+\sqrt{n}}=\frac{\sqrt{n+1}-\sqrt{n}}{\left(\sqrt{n+1}-\sqrt{n}\right)\left(\sqrt{n+1}+\sqrt{n}\right)}=\frac{\sqrt{n+1}-\sqrt{n}}{n+1-n}=\sqrt{n+1}-\sqrt{n}\)
=> \(\frac{1}{2\sqrt{n+1}}< \sqrt{n+1}-\sqrt{n}\)(1)
\(\frac{1}{2\sqrt{n}}=\frac{1}{\sqrt{n}+\sqrt{n}}>\frac{1}{\sqrt{n+1}+\sqrt{n}}=\frac{\sqrt{n+1}-\sqrt{n}}{\left(\sqrt{n+1}-\sqrt{n}\right)\left(\sqrt{n+1}+\sqrt{n}\right)}=\frac{\sqrt{n+1}-\sqrt{n}}{n+1-n}=\sqrt{n+1}-\sqrt{n}\)=> \(\frac{1}{2\sqrt{n}}>\sqrt{n+1}-\sqrt{n}\)(2)
Từ (1) và (2) => \(\frac{1}{2\sqrt{n+1}}< \sqrt{n+1}-\sqrt{n}< \frac{1}{2\sqrt{n}}\)
Đúng 0
Bình luận (0)
Chứng minh bất đẳng thức sau biết a;b;m;n là các số nguyên:
\(a^{m+n}+b^{m+n}\ge a^mb^n+a^nb^m\)
Chứng minh bất đẳng thức Cô-si với n số không âm.
1) chứng minh bất đẳng thức Bu-nhi-a-cốp-ski với bộ n số.
Ai nhanh mình tick!^_^
Chứng minh bất đẳng thức sau
\(\dfrac{1}{n+1}+\dfrac{1}{n+2}+.....+\dfrac{1}{2n}\ge\dfrac{1}{2}\) \(\left(n\in N^{sao}\right)\)
Lời giải:
Tổng trên gồm \([2n-(n+1)]:1+1=n\)\([2n-(n+1)]:1+1=n\)
số hạng
Mỗi số hạng đứng trước \(\frac{1}{2n}\) đều lớn hơn hoặc bằng nó do \(n+1, n+2,....,2n-1\leq 2n\forall n\in\mathbb{N}^*\) thì \(\frac{1}{n+1}, \frac{1}{n+2},..., \frac{1}{2n-1}\geq \frac{1}{2n}\)
Suy ra:
\(\frac{1}{n+1}+\frac{1}{n+2}+...+\frac{1}{2n}\geq \underbrace{\frac{1}{2n}+\frac{1}{2n}+...+\frac{1}{2n}}_{ \text{n lần}}=\frac{n}{2n}=\frac{1}{2}\) (đpcm)
Dấu bằng xảy ra khi \(n=1\)
Đúng 0
Bình luận (0)