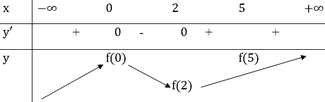
Tìm giá trị lớn nhất và nhỏ nhất của hàm số: f x = x e - x t r ê n n ử a k h o ả n g [ 0 ; + ∞ )

Những câu hỏi liên quan
Tìm giá trị lớn nhất,giá trị nhỏ nhất của hàm số f(x) sau trên đoạn [0;π].Biết f(x)=e^sinx - sinx -1
Xem chi tiết
\(f\left(x\right)=e^{sinx}-sinx-1\)
\(\Rightarrow f'\left(x\right)=cosx.e^{sinx}-cosx=cosx\left(e^{sinx}-1\right)\)
\(f'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sinx=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{\pi}{2}\\x=\pi\end{matrix}\right.\)
\(f\left(0\right)=0\) ; \(f\left(\dfrac{\pi}{2}\right)=e-2\) ; \(f\left(\pi\right)=0\)
\(\Rightarrow f\left(x\right)_{min}=0\) ; \(f\left(x\right)_{max}=e-2\)
Đúng 2
Bình luận (0)
Cho hàm số y f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y f( x) trên [ a; e]? A.
m
a
x
[
a
,...
Đọc tiếp
Cho hàm số y= f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y= f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) = f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y= f( x) trên [ a; e]?
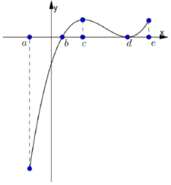
A. m a x [ a , e ] f ( x ) = f ( c ) m i n [ a , e ] f ( x ) = f ( a )
B. m a x [ a , e ] f ( x ) = f ( a ) m i n [ a , e ] f ( x ) = f ( b )
C. m a x [ a , e ] f ( x ) = f ( e ) m i n [ a , e ] f ( x ) = f ( b )
D. m a x [ a , e ] f ( x ) = f ( d ) m i n [ a , e ] f ( x ) = f ( b )
Ta có bảng biến thiên như hình vẽ sau:
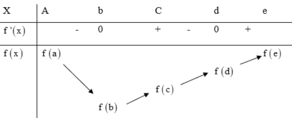
Giá trị nhỏ nhất của hàm số là f( b) nhưng giá trị lớn nhất có thể là f (a) hoặc f( e) Theo giả thiết ta có: f(a) + f( c)) = f( b) + f( d) nên f(a) - f( d)) = f( b) - f( c)< 0
Suy ra : f( a) < f( d) < f( e)
Vậy m a x [ a ; e ] f ( x ) = f ( e ) ; m i n [ a ; e ] f ( x ) = f ( b )
Chọn C.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) liên tục, không âm trên R thỏa mãn
f
(
x
)
.
f
(
x
)
2
x
f
(
x
)
2
+
1
và f(0)0. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số yf(x) trên đoạn [1;3] lần lượt là: A. M20;m2 B. ...
Đọc tiếp
Cho hàm số y=f(x) liên tục, không âm trên R thỏa mãn f ( x ) . f ' ( x ) = 2 x f ( x ) 2 + 1 và f(0)=0. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y=f(x) trên đoạn [1;3] lần lượt là:
A. M=20;m=2
B. M = 4 11 ; m = 3
C. M = 20 ; m = 2
D. M = 3 11 ; m = 3
Cho hàm số yf(x) liên tục trên R có đồ thị như hình vẽ bênTổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số yf(x) trên đoạn [1;4] bằng A. 6 B. 4 C. 5 D. 3
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R có đồ thị như hình vẽ bên
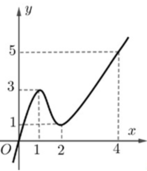
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [1;4] bằng
A. 6
B. 4
C. 5
D. 3
Cho hàm số y f(x) liên tục trên R và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên
-
1
;
3
2
Giá trị của M – m bằng A.
1
2
B. 5 C. 4 D. 3
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên - 1 ; 3 2 Giá trị của M – m bằng
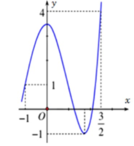
A. 1 2
B. 5
C. 4
D. 3
tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = ( x +3 )( 5 - x ) với -3<= x <=5
f(x) = -x2 + 2x + 15
Đồ thị hàm số là parabol quay xuống dưới, đỉnh parabol tại điểm (1,16), parabol cắt trục hoành tại 2 điểm có hoành độ là -3 và 5 (bạn tự vẽ hình)
Nhìn vào đồ thị suy ra giá trị lớn nhất của f(x) trong [-3,5] là 16 (khi x = 1) và giá trị nhỏ nhất là 0 (khi x = -3 hoặc x=5)
Đúng 0
Bình luận (1)
Cho hàm số f(x) có đạo hàm là hàm f(x). Đồ thị hàm số f(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4]. A. m f(4), M f(2) B. m f(1), M f(2) C. m f(4), M f(1) D. m f(0), M f(2)
Đọc tiếp
Cho hàm số f(x) có đạo hàm là hàm f'(x). Đồ thị hàm số f'(x) như hình vẽ bên. Biết rằng f(0) + f(1) - 2f(2) = f(4) - f(3). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của f(x) trên đoạn [0;4].

A. m = f(4), M = f(2)
B. m = f(1), M = f(2)
C. m = f(4), M = f(1)
D. m = f(0), M = f(2)
Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
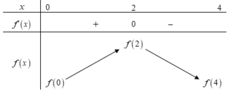
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
![]()
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất và nhỏ nhất của hàm số \(f\left(x\right)=\sqrt{x+1}+\sqrt{3-x}\)
ĐKXĐ : \(-1\le x\le3\)
- ADbu nhi : \(\left(\sqrt{x+1}+\sqrt{3-x}\right)^2\le\left(1^2+1^2\right)\left(\left(\sqrt{x+1}\right)^2+\left(\sqrt{3-x}\right)^2\right)\)
\(=2\left(x+1+3-x\right)=2.4=8\)
\(\Rightarrow\sqrt{x+1}+\sqrt{3-x}\le\sqrt{8}=2\sqrt{2}\)
- Dấu " = " xảy ra \(\Leftrightarrow\dfrac{1}{\sqrt{x+1}}=\dfrac{1}{\sqrt{3-x}}\)
\(\Leftrightarrow x+1=3-x\)
\(\Leftrightarrow x=1\left(TM\right)\)
\(\Rightarrow Max_{f\left(x\right)}=2\sqrt{2}\) tại x = 1.
- Có : \(\sqrt{x+1}+\sqrt{3-x}\ge\sqrt{x+1+3-x}=\sqrt{4}=2\)
- Dấu " = " xảy ra <=> x = -1 ( TM )
\(\Rightarrow Min_{f\left(x\right)}=2\) tại x = - 1 .
Đúng 2
Bình luận (0)
Cho hàm số f(x) có đạo hàm trên R và có đồ thị hàm y f(x) như hình vẽ. Biết rằng
f
(
0
)
+
f
(
3
)
f
(
2
)
+
f
(
5
)
.
Giá trị nhỏ nhất và giá trị lớn của f(x) trên đoạn [0;5] lần lượt là:
A
.
f
(
2
)
;
f
(
0
)...
Đọc tiếp
Cho hàm số f(x) có đạo hàm trên R và có đồ thị hàm y = f'(x) như hình vẽ. Biết rằng f ( 0 ) + f ( 3 ) = f ( 2 ) + f ( 5 ) . Giá trị nhỏ nhất và giá trị lớn của f(x) trên đoạn [0;5] lần lượt là:
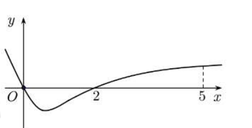
A . f ( 2 ) ; f ( 0 )
B . f ( 0 ) ; f ( 5 )
C . f ( 2 ) ; f ( 5 )
D . f ( 1 ) ; f ( 3 )
Cho hàm số
y
f
(
x
)
xác định và liên tục trên
ℝ
, có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số
y
f
(
x
)
trên đoạn
-
2
;
2
. A. m -5, M 0 B. m -5, M -1 C. m -1, M 0 D. m -2,...
Đọc tiếp
Cho hàm số y = f ( x ) xác định và liên tục trên ℝ , có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = f ( x ) trên đoạn - 2 ; 2
 .
.
A. m = -5, M = 0
B. m = -5, M = -1
C. m = -1, M = 0
D. m = -2, M = 2
Nhận thấy trên đoạn [-2;2]
● Đồ thị hàm số có điểm thấp nhất có tọa độ (-2;-5) và (1;-5)
=> giá trị nhỏ nhất của hàm số này trên đoạn [-2;2] bằng - 5
● Đồ thị hàm số có điểm cao nhất có tọa độ (-1;1) và (-2;1)
=> giá trị lớn nhất của hàm số này trên đoạn [-2;2] bằng -1.
Chọn B.
Đúng 0
Bình luận (0)