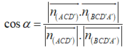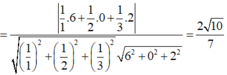Cho hình hộp chữ nhật ABCD.A′B′C′D′ có A B = a , A A ' = 2 a . Biết thể tích hình cầu ngoại tiếp tứ diện ABCD′ là 9 π 2 a 3 . Tính thể tích V của hình chữ nhật ABCD.A′B′C′D′.
A. 4 a 3
B. 4 a 3 3
C. 2 a 3
D. 2 a 3 3
Những câu hỏi liên quan
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có cạnh
AB
a
,
BC
3
a
,
A
C
26
a
.
Thể tích của khối hộp chữ nhật đó là A.
12
a
3
B.
3
a
3
C.
4
a
3...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có cạnh AB = a , BC = 3 a , A ' C = 26 a . Thể tích của khối hộp chữ nhật đó là
A. 12 a 3
B. 3 a 3
C. 4 a 3
D. 6 a 3
Cho hình hộp chữ nhật ABCD.A'B'C'D' có: AB=5cm, BC=4cm,CC'=3cm a, HÃy vẽ hình hộp chữ nhật đó b, Tính thể tích
Cho hình hộp chữ nhật ABCD.A′B′C′D′ABCD.A′B′C′D′ . Tính chu vi ACD′ACD′ biết DD′=4,D′A′=3,D′C′=6DD′=4,D′A′=3,D′C′=6
Cho hình hộp chữ nhật ABCD.A′B′C′D′ABCD.A′B′C′D′ . Tính chu vi ACD′ACD′ biết DD′=4,D′A′=3,D′C′=6DD′=4,D′A′=3,D′C′=6
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB1,BC2,AA3.. Tính sin của góc giữa đường thẳng A′C và mặt phẳng (A′BD). A.
5
91
49
B.
3
14
49
C.
9
14
98
D.
11
70...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=1,BC=2,AA'=3.. Tính sin của góc giữa đường thẳng A′C và mặt phẳng (A′BD).
A. 5 91 49
B. 3 14 49
C. 9 14 98
D. 11 70 98
Cho lăng trụ ABCD.ABCD có ABCD là hình chữ nhật AAABAD. Tính thể tích khối lăng trụ ABCD.ABCD biết AB a , AD asqrt{ }3, AA2aA.3a3 B.a3 C.a3sqrt{ } 3 D.3a3sqrt{ }3Giúp mk với mình cần gấp ạ
Đọc tiếp
Cho lăng trụ ABCD.A'B'C'D' có ABCD là hình chữ nhật A'A=A'B=A'D. Tính thể tích khối lăng trụ ABCD.A'B'C'D' biết AB= a , AD= a\(\sqrt{ }\)3, AA'=2a
A.3a3 B.a3 C.a3\(\sqrt{ }\) 3 D.3a3\(\sqrt{ }\)3
Giúp mk với mình cần gấp ạ
Gọi H là hình chiếu vuông góc của A' lên (ABCD)
Do \(A'A=A'B=A'D\) \(\Rightarrow H\) trùng tâm đường tròn ngoại tiếp tam giác ABD
\(\Rightarrow H\) là trung điểm BD
\(AC=\sqrt{AB^2+AD^2}=2a\)\(\Rightarrow AH=\dfrac{1}{2}AC=a\)
\(\Rightarrow A'H=\sqrt{A'A^2-AH^2}=a\sqrt{3}\)
\(\Rightarrow V=A'H.AB.AD=3a^3\)
Đúng 1
Bình luận (0)
Cho hình hộp chữ nhật ABCD.A’B’C’D’.
a) Chứng minh đường thẳng AD song song với mặt phẳng (A’B’C’D’).
b) Tính thể tích của hình hộp chữ nhật ABCD.A’B’C’D. Biết AB = 3cm, AC = 5cm, AA’ = 2cm.
Giup mik vs
a, Xét mp(AA'D'D) của hình hộp chữ nhật ABCD.A'B'C'D' ta có:
\(AD\text{//}A'D'\) (theo tính chất của hình chữ nhật)
Mà \(A'D'\subset mp\left(A'B'C'D'\right)\) nên \(AD\text{//}mp\left(A'B'C'D'\right)\) (đpcm)
b, Áp dụng định lý Pytago cho ABC vuông tại B ta có:
\(BC=\sqrt{AC^2-AB^2}=\sqrt{5^2-3^3}=4\left(cm\right)\)
Thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là:
\(V=a.b.c=AB.BC.AA'=3.4.2=24\left(cm^3\right)\)
Đúng 0
Bình luận (0)
Giải:
a) Vì đường thẳng AD song song với một trong bốn cạnh của mặt phẳng (A'B'C'D')
Nên đường thẳng AD song song với mặt phẳng (A'B'C'D')
Hay \(AD//mp\left(A'B'C'D'\right)\)
b) Thể tích hình hộp chữ nhật ABCD.A'B'C'D' là:
\(S_{ABCD.A'B'C'D'}=a.b.c=AB.AC.AA'=3.5.2=30\left(cm^3\right)\)
Vậy ...
Đúng 0
Bình luận (0)
a)
AD// mp \(\left(A'B'C'D'\right)\), vì có:
AD \(\notin mp\left(A'B'C'D'\right)\)
AD//A'D'
=>AD// mp \(\left(A'B'C'D'\right)\)( đpcm)
b)
Xét \(\Delta ABC\), có:
Góc ABC = 90o ( tứ giác ABCD là hình chữ nhật)
=> \(\Delta ABC\)\(\perp B\)
Theo định lý Py-ta-go, ta có:
\(AC^2=AB^2+BC^2\)
\(\Rightarrow BC=\sqrt{5^2-3^2}=4\left(cm\right)\)
\(\Rightarrow V_{ABCD.A'B'C'D'}=3.4.2=24\left(cm^3\right)\)
Đúng 0
Bình luận (2)
Xem thêm câu trả lời
Cho hình hộp chữ nhật ABCD.A B C D có các kích thước là AB2, AD3, AA4. Gọi (N) là hình nón có đỉnh là tâm của mặt ABB A và đường tròn đáy là đường tròn ngoại tiếp hình chữ nhật. Thể tích của khối nón (N) là A.
5
π
B.
13
π
3
C.
8
π
D.
25
π
6
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A' B' C' D' có các kích thước là AB=2, AD=3, AA'=4. Gọi (N) là hình nón có đỉnh là tâm của mặt ABB' A' và đường tròn đáy là đường tròn ngoại tiếp hình chữ nhật. Thể tích của khối nón (N) là
A. 5 π
B. 13 π 3
C. 8 π
D. 25 π 6
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB1, BC2, AA3. Côsin góc giữa hai mặt phẳng (ACD′) và (BCD′A′) bằng A.
2
10
7
B.
3
7
C.
3
35...
Đọc tiếp
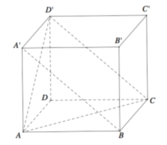
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=1, BC=2, AA'=3. Côsin góc giữa hai mặt phẳng (ACD′) và (BCD′A′) bằng
A. 2 10 7
B. 3 7
C. 3 35 35
D. 910 35
Đáp án A
Chọn gốc tọa độ tại D, các tia Ox, Oy, Oz trùng với các tia DC,DA,DD'.
Và B(1;2;0)
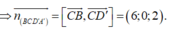
Do đó
Đúng 0
Bình luận (0)