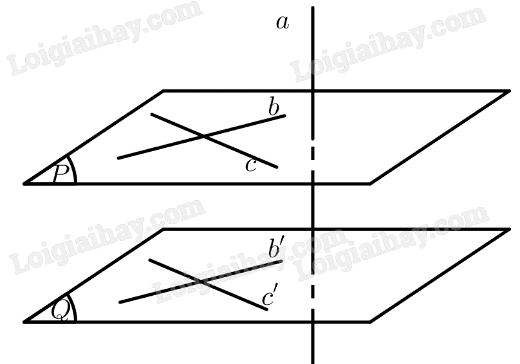
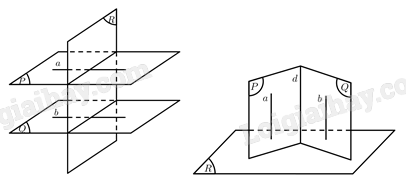
Trong không gian, tìm mệnh đề SAI trong các mệnh đề sau:
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt thẳng thì song song với nhau
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau
C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau
D. Hai mặt phẳng phân biệt cùng song song với một đường thẳng thì song song với nhau