Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa các cặp vectơ sau đây:
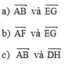
cho hình lập phương ABCD.EFGH hát Hãy xác định góc giữa cặp vectơ vectơ AB và vectơ DH
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ AB và EG?
A. 90 o
B. 60 o
C. 45 o
D. 120 o
Ta có. EG//AC (do ACGE là hình chữ nhật)

⇒ A B , E G = A B , A C = B A C = 45 o
Đáp án cần chọn là C
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ A B → v à E G → ?

A. 90 o
B. 60 o
C. 45 o
D. 120 o
Đáp án C
Ta có. EG//AC (do ACGE là hình chữ nhật)
![]()
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vecto A B → và E G →
A. 90 °
B. 60 °
C. 45 °
D. 120 °
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa các cặp vectơ sau đây :
a) \(\overrightarrow{AB}\) và \(\overrightarrow{EG}\)
b) \(\overrightarrow{AF}\) và \(\overrightarrow{EG}\)
c) \(\overrightarrow{AB}\) và \(\overrightarrow{DH}\)
a. Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa 2 đường thẳng AC và AH
b. Cho hình lập phương ABCD.A'B'C'D'. Số do góc giữa 2 đường thẳng A'B và B'C là?
c. Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I vàJ lần lượt là trung điểm của SC và BC. Số đo góc (IJ,CD) là?
d. Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa 2 vecto AF và EG?
a. Gọi cạnh lập phương là a
Ta có: \(AC=\sqrt{AB^2+AD^2}=a\sqrt{2}\)
\(AH=\sqrt{AD^2+DH^2}=a\sqrt{2}\)
\(CH=\sqrt{CD^2+DH^2}=a\sqrt{2}\)
\(\Rightarrow\Delta ACH\) đều \(\Rightarrow\widehat{CAH}=60^0\)
b.
Do \(B'C||A'D\Rightarrow\) góc giữa A'B và B'C bằng góc giữa A'B và A'D
Tương tự câu a, ta có tam giác A'BD đều \(\Rightarrow\widehat{BA'D}=60^0\)
c.
Do IJ song song SB (đường trung bình), CD song song AB \(\Rightarrow\) góc giữa IJ và CD bằng góc giữa SB và AB
Tam giác SAB đều (các cạnh bằng a) \(\Rightarrow\widehat{SBA}=60^0\)
d.
\(\overrightarrow{EG}=\overrightarrow{AC}\Rightarrow\widehat{\left(\overrightarrow{AF};\overrightarrow{EG}\right)=\widehat{\left(\overrightarrow{AF};\overrightarrow{AC}\right)}=\widehat{FAC}=60^0}\) do tam giác FAC đều
Cho hình chóp S.ABC có SA = SB = SC và A S B ^ = B S C ^ = C S A ^ . Hãy xác định góc giữa cặp vectơ S B → và A C → ?
A. 60°
B. 120°
C. 45°
D. 90°
Chọn D.
Cách 1:
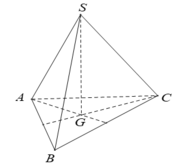
- Ta có: SA = SB = SC nên:
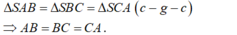
- Do đó, tam giác ABC đều. Gọi G là trọng tâm của tam giác ABC.
- Vì hình chóp S.ABC có SA = SB = SC nên hình chiếu của S trùng với G. Hay SG ⊥ (ABC).
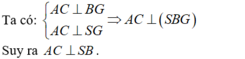
- Vậy góc giữa cặp vectơ 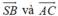 bằng 90°.
bằng 90°.
Cách 2:
- Ta có:
Cho hình chóp S.ABC có SA = SB = SC và A S B ^ = B S C ^ = C S A ^ . Hãy xác định góc giữa cặp vectơ S B → và A C → ?
A. 60°
B. 120°
C. 45°
D. 90°
Chọn D.
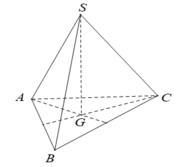
Cách 1:
- Ta có: SA = SB = SC nên:
- Do đó, tam giác ABC đều. Gọi G là trọng tâm của tam giác ABC.
- Vì hình chóp S.ABC có SA = SB = SC nên hình chiếu của S trùng với G. Hay SG ⊥ (ABC).
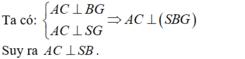
- Vậy góc giữa cặp vectơ 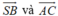 bằng 90°.
bằng 90°.
Cách 2:
- Ta có:
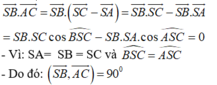
Cho tứ diện ABCD có AB = AC = AD = a và B A C ^ = B A D ^ = 60 ° . Hãy xác định góc giữa cặp vectơ A B → , C D →
A. 60 °
B. 45 °
C. 120 °
D. 90 °