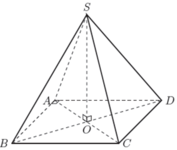
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng a 2 , S A = 2 a . Côsin của góc giữa (SDC) và (SAC) bằng:
A. 21 14
B. 21 3
C. 21 2
D. 21 7
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng a 2 , S A = 2 a . Côsin của góc giữa (SDC) và (SAC) bằng:
A. 21 14
B. 21 3
C. 21 2
D. 21 7
Đáp án D
Ta có A C = 2 a = S A = S C suy ra tam giác SAC đều, do đó S O = 2 a 3 2 = a 3 . Vẽ D J ⊥ S C , J ∈ S C . Khi đó BJ vuông góc với SC.
Ta có: S C D ∩ S C A = S C , J D ⊥ S C , J B ⊥ S C . Đặt δ = D J B ^ . Vì JD = JB nên JO là đường cao của tam giác cân DJB, suy ra JO cũng là đường phân giác. Do đó góc giữa (SDC) và (SAC) là D I O ^ = δ 2 .
Ta có S C ⊥ D J B , mà O J ⊂ D J B nên O J ⊥ S C . Trong Δ D J O ta có: O J = O D . cot δ 2 . Trong Δ S O C ta có: 1 O J 2 = 1 O S 2 + 1 O A 2 ⇔ 1 a 2 cot 2 δ 2 = 1 3 a 2 + 1 a 2
Do đó: 1 a 2 cot 2 δ 2 = 4 3 a 2 ⇔ cot 2 δ 2 = 3 4 ⇔ 1 + cot 2 δ 2 = 7 4
⇔ 1 sin 2 δ 2 = 7 4 ⇔ sin 2 δ 2 = 4 7 ⇔ cos 2 δ 2 = 3 7
Mà cos δ 2 > 0 nên từ (1) ta có cos δ 2 = 21 7 . Vậy côsin của góc giữa (SDC) và ( S A C ) bằng 21 7
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với (ABCD). Biết rằng côsin của góc giữa (SCD) và (ABCD) bằng 2 19 19 . Tính theo a thể tích V của khối chóp S.ABCD.
A. V = 19 a 3 6
B. V = 15 a 3 6
C. V = 19 a 3 2
D. V = 15 a 3 6
Đáp án B
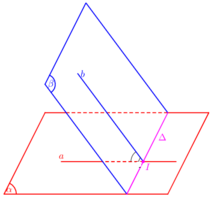
Phương pháp:
Xác định góc giữa hai mặt phẳng (α;β)
- Tìm giao tuyến Δ của (α;β)
- Xác định 1 mặt phẳng γ ⊥ Δ
- Tìm các giao tuyến a = α∩γ, b = β ∩ γ
- Góc giữa hai mặt phẳng (α;β):(α;β) = (a;b)
Cách giải:
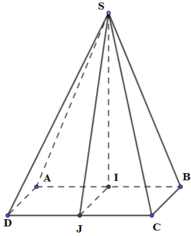
Gọi I, J lần lượt là trung điểm của AB, CD.
Tam giác SAB cân tại S ⇒ SI ⊥ AB
Vì mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD) nên SI ⊥ (ABCD)
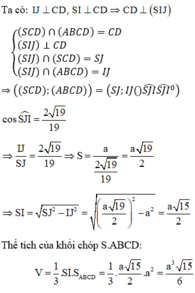
Hình chóp S.ABCD có đáy ABCDa là hình vuông cạnh a, SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy (ABCD). Biết côsin của góc tạo bởi mặt phẳng (SCD) và (ABCD) bằng 2 17 17 . Thể tích Vcủa khối chóp S.ABCD là:
A. V = a 3 13 6
B. V = a 3 17 6
C. V = a 3 17 2
D. V = a 3 13 2
Cho khối chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, đường cao SO. Biết SO = a 2 2 thể tích khối chóp S.ABCD bằng:
A. a 3 2 6
B. a 3 2 3
C. a 3 2 2
D. a 3 3 4
Cho khối chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, đường cao SO. Biết S O = a 2 2 , thể tích khối chóp S.ABCD bằng:
A. a 3 2 6 .
B. a 3 2 3 .
C. a 3 2 2 .
D. a 3 3 4 .
Bài 10. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng a * sqrt(3) . O là tâm hình vuông 1/ Chứng minh :a) (SAC) I (ABCD) b) (SAC) (SBD). 2 / a ) Tính d(S; (ABCD)) b) Tính d(O; (SCD)) 3/ Tính góc giữa:a) SC và (ABCD); b) (SAB) và (ABCD).
a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
b: AC vuông góc BD
BD vuông góc SO
=>BD vuông góc (SAC)
=>(SBD) vuông goc (SAC)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng a√3 . O là tâm hình vuông . Chứng minh (SAC) vuông góc (ABCD) ; (SAC) vuông góc (SBD)
Do S.ABCD là chóp tứ giác đều \(\Rightarrow SO\perp\left(ABCD\right)\)
Mà \(O\in AC\Rightarrow SO\in\left(SAC\right)\Rightarrow\left(SAC\right)\perp\left(ABCD\right)\)
Ta có: \(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp BD\\AC\perp BD\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Mà \(BD\in\left(SBD\right)\Rightarrow\left(SBD\right)\perp\left(SAC\right)\)
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO = a. Khoảng cách từ O đến mặt phẳng (SCD) bằng
A. 2 a 2
B. 3 a
C. 5 a 5
D. 6 a 3
Chọn A

Vẽ OE vuông góc CD, vẽ OH vuông góc với DE
Ta có
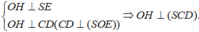
Tam giác vuông cân tại O, có
SO = OE = a
![]()
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh 2a, tâm O, SO = a. Khoảng cách từ O đến mặt phẳng (SCD) bằng
A. 3 a
B. 5 a 5
C. 6 a 3
D. 2 a 2