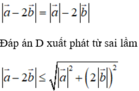Cho hai vectơ a → , b → thỏa mãn a → + b → = 0 . Khẳng định nào sau đây là đúng?
A. a → = - b →
B. a → = b →
C. a → + b → = 0
D. a → = b → = 0
Cho hai vectơ a → ; b → thỏa mãn a → = 3 , b → = 2 và a → b → = - 3 . Xác định góc giữa hai vectơ đó
A. 300
B. 600
C. 1350
D. 1200
Cho hai vectơ a → và b → thỏa mãn a → = 3, b → = 2 và a → . b → = − 3. Xác định góc α giữa hai vectơ a → và b →
A. α = 30 0 .
B. α = 45 0 .
C. α = 60 0 .
D. α = 120 0 .
a → . b → = a → . b → . c o s a → , b → ⇒ c o s a → , b → = a → . b → a → . b → = − 3 3.2 = − 1 2 ⇒ a → , b → = 120 0 .
Đáp án D
Cho hai vectơ a → và b → thỏa mãn a → = 3, b → = 2 và a → . b → = − 3. Xác định góc α giữa hai vectơ a → và b →
A. α = 30 0 .
B. α = 45 0 .
C. α = 60 0 .
D. α = 120 0 .
Ta có a → . b → = a → . b → . c o s a → , b → .
⇒ c o s a → , b → = a → . b → a → . b → = − 3 3.2 = − 1 2 ⇒ a → , b → = 120 0
Chọn D.
Cho hai vectơ a → , b → thỏa mãn: a → = 4 ; b → = 3 ; a → − b → = 4 . Gọi α là góc giữa hai vectơ a → , b → . Chọn phát biểu đúng.
A. α = 60 0 .
B. α = 30 0 .
C. cos α = 1 3 .
D. cos α = 3 8 .
Đáp án là D
Ta có a → − b → = 4 ⇒ a → − b → 2 = 16
⇒ a → 2 + b → 2 − 2 a → b → = 16
⇒ 2 a → b → = a → 2 + b → 2 − 16 = 4 2 + 3 2 − 16 = 9
⇒ a → b → = 9 2
Từ đó suy ra cos a → , b → = a → b → a → b → = 3 8 .
Cho hai vectơ a → , b → khác vectơ 0 → , không cùng phương và có độ dài bằng nhau. Khi đó giá của hai vectơ a → + b → và a → - b → thỏa mãn điều kiện nào sau đây?
A. Cắt và không vuông góc
B. Vuông góc với nhau
C. Song song với nhau
D. Trùng nhau
Câu 4 : Cho tam giác ABC vuông cân tại A và AB =√2 . Tính vectơ CA . vectơ BC . Câu 5 : Cho ABC có trọng tâm G . Biểu diễn vectơ AG theo hai vectơ AB , AC được kết quả là? Câu 6 : Cho các vectơ a,b thỏa mãn|vectơ a | =1 , |vectơ B | =2 , | vectơ a - vectơ b| =3 . Tích vectơ a. vectơ b bằng? Câu 7 : Cho hình vuông ABCD có cạnh bằng a . Tính| vectơ AB - vectơ AD + vectơ CD | .
Câu 4:
Áp dụng định lý Pytago
\(BC^2=AB^2+AC^2\Rightarrow BC=2\)
Ta có:
\(\overrightarrow{CA}.\overrightarrow{BC}=-\overrightarrow{CA}.\overrightarrow{CB}=-\dfrac{CA^2+CB^2-AB^2}{2}=-\dfrac{2+4-2}{2}=-2\)
Câu 5:
Gọi M là trung điểm BC
\(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
Mà: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
Câu 6:
\(\left|\overrightarrow{a}-\overrightarrow{b}\right|=3\)
\(a^2+b^2-2\overrightarrow{a}.\overrightarrow{b}=9\)
\(\overrightarrow{a}.\overrightarrow{b}=\dfrac{1^2+2^2-9}{2}=-2\)
Câu 7:
\(\left|\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{CD}\right|=\left|\overrightarrow{DB}+\overrightarrow{CD}\right|\)
\(=\left|\overrightarrow{DB}-\overrightarrow{DC}\right|=\left|\overrightarrow{CB}\right|=BC=a\)
Cho hai vectơ a → ; b → thỏa mãn a → = 4 , b → = 5 , a → , b → = 120 ° . Giá trị của tích vô hướng a → . b → là:
A. 10
B. -10
C. 10 3
D. - 10 3
a → . b → = a → . b → . cos a → , b → = 4.5. cos 120 ° = 4.5. − 1 2 = − 10
Chọn B.
Cho hai vectơ
a
→
,
b
→
thay đổi nhưng luôn thỏa mãn: ![]() Giá trị nhỏ nhất của
Giá trị nhỏ nhất của ![]()
A. 11
B. -1
C. 1
D. 0
Đáp án C
Áp dụng bất đẳng thức vectơ
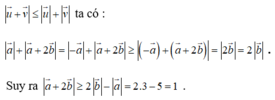
Dấu bằng xảy ra khi 2 vectơ ![]() cùng hướng. Vậy độ dài của vectơ |
a
→
-
2
b
→
| ≥ 0 nhỏ nhất bằng 1.
cùng hướng. Vậy độ dài của vectơ |
a
→
-
2
b
→
| ≥ 0 nhỏ nhất bằng 1.
Suy ra đáp án đúng là C.
Cho hai vectơ
a
→
,
b
→
thay đổi nhưng luôn thỏa mãn ![]()
Giá trị nhỏ nhất của ![]()
A. 11
B. -1
C. 1
D. 61
Đáp án A
Sử dụng bất đẳng thức vectơ:
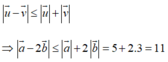
Dấu bằng xảy ra khi và chỉ khi hai vectơ này ngược hướng. Suy ra đáp án A.
Hai đáp án B và C xuất phát từ sai lầm