Tọa độ giao điểm của đường thẳng d : x = 1 + 2 t y = 2 + 2 t và đường tròn (C): (x-1 ) 2 + (y-2 ) 2 = 32 là:

Những câu hỏi liên quan
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng
d
:
x
1
+
t
y
2
+
3
t
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d : x = 1 + t y = 2 + 3 t z = 3 - t , d ' : x = 2 - 2 t ' y = - 2 + t ' z = 1 + 3 t ' . Tìm tọa độ giao điểm M của hai đường thẳng d và d’
A. M(-1;0;4)
B. M(4;0;-1)
C. M(0;4;-1)
D. M(0;-1;4)
tìm tọa độ giao điểm của các đường thẳng sau với Ox(d):=y=x-2 (d'):y=-x+2.Vẽ hai đường thẳng trên cùng mặt phẳng tọa dộ xác định toạn độ giao điểm của (d) và (d').Nhận xét gì về hai đường thẳng trên
Tọa độ giao điểm là:
x-2=-x+2 và y=x-2
=>x=2 và y=0
Vì 1*(-1)=-1
nên (d) vuông góc với (d')
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d:
x
1
+
t
y
2
+
3
t...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d: x = 1 + t y = 2 + 3 t z = 3 - t và d': x = 2 - 2 t ' y = - 2 - t ' z = 1 + 3 t ' . Tìm tọa độ M giao điểm của d và d'.
![]()
![]()
![]()
![]()
Tọa độ giao điểm của hai đường thẳng d: x - 3y - 1 0;
d
x
2
t
y
3
-
t
là: A. (1;4) B. (-1;4) C. (4;1) D. (4;-1)
Đọc tiếp
Tọa độ giao điểm của hai đường thẳng d: x - 3y - 1 = 0; d ' = x = 2 t y = 3 - t là:
A. (1;4)
B. (-1;4)
C. (4;1)
D. (4;-1)
Đáp án: C
Gọi M là giao điểm của d và d’
Vì M ∈ d' ⇒ M(2t; 3-t)
Vì M ∈ d ⇒ 2t - 3.(3 - t) - 1 = 0 ⇔ 2t - 9 + 3t - 1 = 0 ⇔ t = 2 ⇒ M(4;1)
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-1;1;2), B(0;1;1), C(1;0;4) và đường thẳng
d
:
x
-
t
y
2
+
t
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-1;1;2), B(0;1;1), C(1;0;4) và đường thẳng d : x = - t y = 2 + t z = 3 - t . Tọa độ giao điểm của mặt phẳng (ABC) và đường thẳng d là
![]()
![]()
![]()
![]()
Cho parabol (P) \(y=x^2\), đường thẳng (d) y =2x + m.
a) Vẽ parabol và đường thẳng (d) khi m = 3. Tìm tọa độ giao điểm
b) Tìm m để đường thẳng (d) tiếp xúc với (P). Tìm tọa độ giao điểm
a: Khi m=3 thì (d); y=2x+3
Phương trình hoành độ giao điểm là:
x2-2x-3=0
=>(x-3)(x+1)=0
=>x=3 hoặc x=-1
Khi x=3 thì y=9
Khi x=-1thì y=1
b: PTHDGĐ là:
\(x^2-2x-m=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot1\cdot\left(-m\right)=4m+4\)
Để (d) tiếp xúc với (P) thì 4m+4=0
=>m=-1
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d:
x
1
-
t
y
2
t
z
2
+
2...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d: x = 1 - t y = 2 t z = 2 + 2 t , t ∈ ℝ và mặt phẳng (P): x + y -z -1 = 0 Giao điểm M của d và (P) có tọa độ là
A. M(1;0;2)
B. M(3;−4;−2)
C. M(0;2;4)
D. M(1;1;1)
Chọn B

Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).
Đúng 0
Bình luận (0)
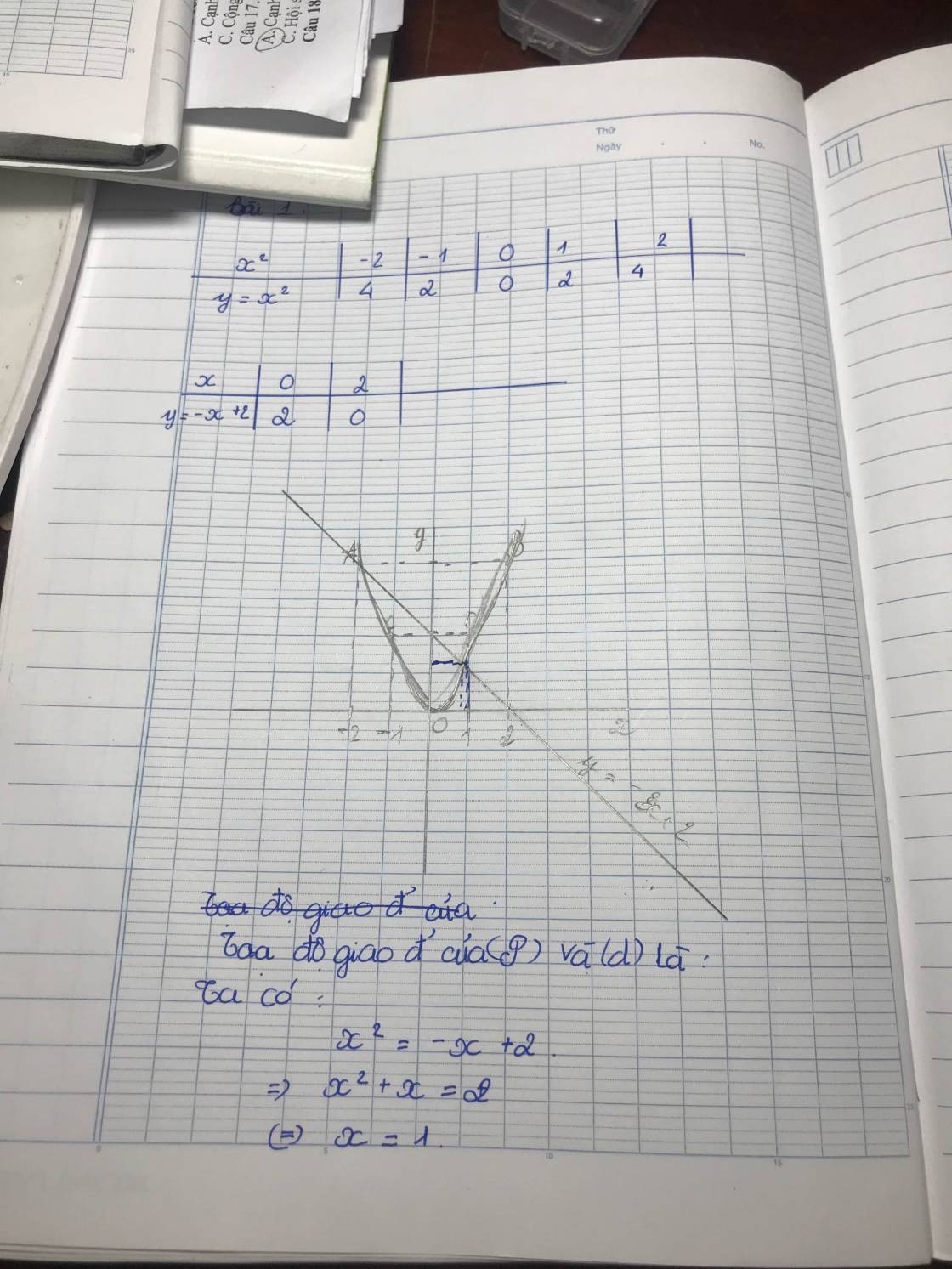
(2,5 điểm) Trong mặt phẳng tọa độ $Oxy$, cho parabol $(P): y=x^2$ và đường thẳng $(d):y=-x+2$.
1. Tìm tọa độ giao điểm của $(P)$ và $(d)$.
2. Gọi $A$, $B$ là hai giao điểm của $(P)$ và $(d)$. Tính diện tích tam giác $OAB$.
Phương trình hoành độ giao điểm
x2 = -x + 2
<=> x2 + x - 2 = 0
Nhận thấy phương trình có a + b + c = 0 nên phương trình có 2 nghiệm \(x_1=1;x_2=-2\)
Với x1 = 1 => y1 = 1 => A(1,1)
Với x2 = -2 => y2 = 4 => B(-2 , 4)
Ta có BO = \(\sqrt{\left(-2\right)^2+4^2}=\sqrt{20}\);
\(OA=\sqrt{1^2+1^2}=\sqrt{2}\)
AB = \(\sqrt{3^2+3^2}=\sqrt{18}\)
Từ đó dễ thấy OA2 + AB2 = BO2
=> Tam giác AOB vuông tại A
nên SAOB = \(\dfrac{\sqrt{18}.\sqrt{2}}{2}=3\)
x2 = -x + 2
<=> x2 + x - 2 = 0
Nhận thấy phương trình có a + b + c = 0 nên phương trình có 2 nghiệm
Với x1 = 1 => y1 = 1 => A(1,1)
Với x2 = -2 => y2 = 4 => B(-2 , 4)
Ta có BO = ;
AB =
Từ đó dễ thấy OA2 + AB2 = BO2
=> Tam giác AOB vuông tại A
nên SAOB =
Đúng 1
Bình luận (0)
xét pt hoành độ giao điểm của (p) và (d) ta dc
x2
Đúng 0
Bình luận (0)
cho parabol (p) : y=\(-\dfrac{x^2}{2}\)và đường thẳng y=\(-\dfrac{1}{2}x-1\) (d) trên cùng mặt tọa độ .a) vẽ parabol (P) và đường thẳng (d) trên cùng hệ trục tọa độ Oxy
b)tìm tọa độ giao điểm của (p) và (d) bằng phép tính
b: Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{2}x^2=-\dfrac{1}{2}x-1\)
\(\Leftrightarrow-\dfrac{1}{2}x^2+\dfrac{1}{2}x+1=0\)
\(\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Thay x=2 vào (P), ta được:
\(y=\dfrac{-2^2}{2}=-2\)
Thay x=-1 vào (P), ta được:
\(y=-\dfrac{1^2}{2}=-\dfrac{1}{2}\)
Đúng 2
Bình luận (0)
Bài 8: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d:left{{}begin{matrix}x-2-2ty1+2tend{matrix}right.left(tin Rright) và điểm A(3;1).1) Viết phương trình đường thẳng d’ đi qua A và vuông góc với đường thẳng d.2) Tìm tọa độ giao điểm H của đường thẳng d và d’.3) Xác định tọa độ điểm A’ đối xứng với A qua đường thẳng d.4) Tìm tọa độ điểm M nằm trên đường thẳng d sao cho tổng khoảng cách MA+MO là nhỏ nhất.5) Viết phương trình đường tròn (C) có tâm I nằm trên đường thẳng d và đi qua hai điểm A, O.
Đọc tiếp
Bài 8: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d:\(\left\{{}\begin{matrix}x=-2-2t\\y=1+2t\end{matrix}\right.\left(t\in R\right)\) và điểm A(3;1).
1) Viết phương trình đường thẳng d’ đi qua A và vuông góc với đường thẳng d.
2) Tìm tọa độ giao điểm H của đường thẳng d và d’.
3) Xác định tọa độ điểm A’ đối xứng với A qua đường thẳng d.
4) Tìm tọa độ điểm M nằm trên đường thẳng d sao cho tổng khoảng cách MA+MO là nhỏ nhất.
5) Viết phương trình đường tròn (C) có tâm I nằm trên đường thẳng d và đi qua hai điểm A, O.
1: (d): x=-2-2t và y=1+2t nên (d) có VTCP là (-2;2)=(-1;1) và đi qua B(-2;1)
=>(d') có VTPT là (-1;1)
Phương trình (d') là;
-1(x-3)+1(y-1)=0
=>-x+3+y-1=0
=>-x+y+2=0
2: (d) có VTCP là (-1;1)
=>VTPT là (1;1)
Phương trình (d) là:
1(x+2)+1(y-1)=0
=>x+y+1=0
Tọa độ H là;
x+y+1=0 và -x+y+2=0
=>x=1/2 và y=-3/2
Đúng 1
Bình luận (0)