Trong không gian Oxyz, cho hai đường thẳng:
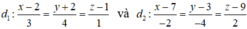
Cho M là một điểm di động trên d 1 , N là một điểm di động trên d 2 . Khoảng cách nhỏ nhất của đoạn thẳng MN là:
A. 3 14
B. 3 14
C. 6 14
D. 0
Trong không gian Oxyz, cho đường thẳng d : x = 4 - 3 t y = 3 + 4 t z = 0 . Gọi A là hình chiếu vuông góc của O trên d. Điểm M di động trên tia Oz, điểm N di động trên đường thẳng d sao cho MN = OM + AN. Gọi I là trung điểm của đoạn thẳng OA. Trong trường hợp diện tích tam giác IMN đạt giá trị nhỏ nhất, một vectơ pháp tuyến của mặt phẳng (M, d) có tọa độ là
A. 4 ; 3 ; 5 2
B. 4 ; 3 ; 10 2
C. 4 ; 3 ; 5 10
D. 4 ; 3 ; 10 10
Trong không gian Oxyz, cho hai mặt phẳn song song (P): Ax + By + Cz + D = 0 và (Q): Ax + By + Cz + D' = 0. M là một điểm di động trên mặt phẳng (P). Khẳng định nào dưới đây có thể sai?
A. Khoảng cách từ điểm M đến mặt phẳng (Q) không phụ thuộc vào M.
B. Khoảng cách giữa hai mặt phẳng (P) và (Q) chính là khoảng cách từ M đến mặt phẳng (Q)
C. Khoảng cách giữa hai mặt phẳng (P) và (Q) là 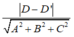
D. Khoảng cách giữa hai mặt phẳng (P) và (Q) là |D' - D|
Đáp án D
Nếu hai mặt phẳng (P) và (Q) song song với nhau và M thuộc mặt phẳng (P) thì:
+ Khoảng cách từ điểm M đến mặt phẳng (Q) không phụ thuộc vào M.
+ Khoảng cách giữa hai mặt phẳng (P) và (Q) chính là khoảng cách từ M đến mặt phẳng (Q)
+ Khoảng cách giữa hai mặt phẳng (P) và (Q) là 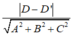
+ Đặc biệt, khoảng cách giữa hai mặt phẳng (P) và (Q) là |D - D'| khi và chỉ khi:
A 2 + B 2 + C 2 =1
Do đó, mệnh đề D có thể sai.
Trong không gian với hệ tọa độ Oxyz, cho điểm A(-2;1;5) và hai mặt phẳng (P): 2x + y + 3z - 7 = 0, (Q): 3x - 2y - z + 1 = 0. Gọi M là điểm nằm trên mặt phẳng (P) và điểm N nằm trên mặt phẳng (Q) thỏa mãn A M → = 2 A N → . Khi M di động trên mặt phẳng (P) thì quỹ tích điểm N là một đường thẳng có phương trình là
A. x = - 3 - 5 t y = - 1 + 11 t z = 6 - 7 t
B. x = 1 + 7 t y = - 8 - 5 t z = 6 - 7 t
C. x = 7 + 11 t y = - 8 - 5 t z = - 8 - 7 t
D. x = 2 + 5 t y = 3 + 11 t z = - 1 - 7 t
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x+2y-z+16=0 và mặt cầu (s): (x-2)2 + (y+1)2 + (z-3)2=9. Điểm M di động trên trên (S) và điểm N di động trên (P) sao cho độ dài đoạn thẳng MN ngắn nhất. Tọa độ điểm M là
A. M(0;1;-1)
B. M(0;-3;4)
C. M(2;0;1)
D. M(-2;2;-3)
Trong không gian tọa độ Oxyz, cho đường thẳng d : x 2 = y - 1 1 = z + 1 - 1 và điểm A 1 ; 1 ; 1 . Hai điểm B, C di động trên đường thẳng d sao cho mặt phẳng O A B vuông góc với O A C . Gọi điểm B’ là hình chiếu vuông góc của điểm B lên đường thẳng AC. Biết quỹ tích các điểm B’ là một đường tròn cố định, tính bán kính r của đường tròn này.
A. r = 60 10
B. r = 3 5 10
C. r = 70 10
D. r = 3 5 5
Chọn đáp án B
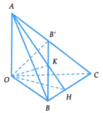

trên H là hình chiếu của O lên đường thẳng d.

Suy ra điểm B’ thuộc đường tròn đường kính AK, đường tròn này vẽ trong mặt phẳng (A,d)

Cách 2: Vì B’ là hình chiếu của B lên AC nên A B ' ⊥ O B ' , suy ra B’ thuộc mặt cầu (S), đường kính AO.

Trong không gian Oxyz, cho hai điểm A(5;0;0), B(3;4;0). Với C là điểm nằm trên trục Oz, gọi H là trực tâm của tam giác ABC. Khi C di động trên trục Oz thì H luôn thuộc một đường tròn cố định. Bán kính đường tròn đó là
A. 5 4
B. 3 2
C. 5 2
D. 3
Trong không gian Oxyz, cho hai điểm A(5;0;0), B(3;4;0). Với C là điểm nằm trên trục Oz, gọi H là trực tâm của tam giác ABC. Khi C di động trên trục Oz thì H luôn thuộc một đường tròn cố định. Bán kính đường tròn đó là
A. 5 4
B. 3 2
C. 5 2
D. 3
Đáp án A

Gọi K là trực tâm của tam giác OAB
Và M là trung điểm của AB=>OM ⊥ AB vì tam giác OAB cân
Mà H là trực tâm của tam giác ABC => HK ⊥ (ABC)
Suy ra HK ⊥ HM => H thuộc đường tròn đường kính KM
Ta có trung điểm M của AB là M(4;2;0)
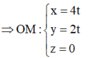
![]()
![]()
![]()

Vậy bán kính đường tròn cần tính
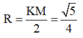
Trong không gian Oxyz, cho điểm A di động trên mặt phẳng (P): 2x - y - 2z = 0, điểm B di động trên mặt phẳng (Q): 4x - 2y - 4z - 9 = 0. Khoảng cách giữa hai điểm A và B nhỏ nhất là:
A. 3 2
B. 1 4
C. 9 28
D. 9 28
Đáp án A
Khoảng cách nhỏ nhất giữa hai điểm A và B chính là khoảng cách giữa hai mặt phẳng (P) và (Q), dấu bằng xày ra khi và chỉ khi AB vuông góc với (P). Mặt khác vì O thuộc (P) nên ta có:
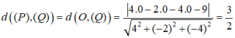
Vậy khoảng cách giữa hai điểm A và B nhỏ nhất bằng 3/2
Trong không gian Oxyz, cho hai mặt cầu (S) và (S’) có tâm lần lượt là I(-1;2;3), I’(3;-2;1) và có bán kính lần lượt là 4 và 2. Cho điểm M di động trên mặt cầu (S), N di động trên mặt cầu (S’). Khi đó giá trị lớn nhất của đoạn thẳng MN bằng:
A. 8
B. 2
C. 12
D. 6
Đáp án C
Ta có: II' = 6 = R + R'
Ta có: MN ≥ MI + II' + I'N = R + 6 + R' = 12
Dấu bằng xảy ra khi M, I, I', N theo thứ tự nằm trên một đường thẳng. Do đó M là giao điểm của tia đối của tia II' với mặt cầu (S), N là giao điểm của tia đối của tia I’I với mặt cầu (S’). Vậy đáp án đúng là C.