Trong các hình sau, hình nào là hình chóp cụt?
A. 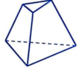
B.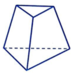
C.
D. 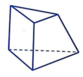
Trong các hình sau, hình nào là hình chóp cụt?
A.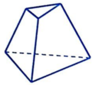
B.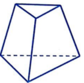
C.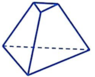
D.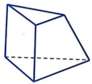
Đáp án C.
+ Hình A: Tồn tại mặt bên không phải hình thang.
+ Hình B: Các cạnh bên không đồng quy.
+ Hình D: Các cạnh bên không đồng quy.
+ Hình C: Các mặt bên là các hình thang và các cạnh bên đồng quy nên C là hình chóp cụt.
Trong các hình sau, hình nào là hình chóp cụt?
A. 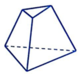
B. 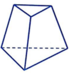
C. 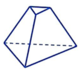
D. 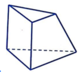
Đáp án C.
+ Hình A: Tồn tại mặt bên không phải hình thang.
+ Hình B: Các cạnh bên không đồng quy.
+ Hình D: Các cạnh bên không đồng quy.
+ Hình C: Các mặt bên là các hình thang và các cạnh bên đồng quy nên C là hình chóp cụt.
Cho hình chóp cụt đều ABCD.A'B'C'D'. Gọi M, N theo thứ tự là trung điểm của các cạnh BC, B’C. Cho biết AB = 4 cm, A'B' = 8 cm và MN = 4 cm.
a) Tính diện tích toàn phần hình chóp cụt.
b) Tính chiều cao hình chóp cụt.
c) Lắp một hình chóp đều có độ dài đáy bằng đúng độ dài đáy nhỏ hình chóp cụt. Cho biết cạnh bên hình chóp đều bằng 2 5 c m , hãy tính thể tích của hình chóp đều mói sau khi lắp ghép.
Tìm các mặt phẳng đối xứng của các hình sau đây : a) Hình chóp tứ giác đều ; b) Hình chóp cụt tam giác đều ; c) Hình hộp chữ nhật mà không có mặt nào là hình vuông.
Các mặt phẳng đối xứng của hình chóp tứ giác đều S.ABCDS.ABCD là các mặt phẳng:
– Mp(SAC)(SAC)
– Mp(SBD)(SBD)
Cho hình chóp cụt tứ giác đều ABCD.A'B'C'D' có các cạnh đáy là a và 2 a, chiều cao của mặt bên là a
a) Tính diện tích xung quanh của hình chóp cụt
b) Tính độ dài cạnh bên và chiều cao hình chóp cụt
\(a,S_{xp}=4.\dfrac{a+2a}{2}.a=6a^2\)
\(b,\)Vẽ một mặt bên. Ta có:\(AH=\dfrac{AB-A^'B^'}{2}=\dfrac{2a-a}{2}=\dfrac{a}{2}\)
Trong tamn giác vuông A'HA:
\(AA^'=\sqrt{a^2+\left(\dfrac{a}{2}\right)^2}=\sqrt{\dfrac{5a^2}{4}}\)
Từ đó tính tiếp sẽ ra chiều cao hình chóp
Đáp số :Độ dài cạnh bên là :\(\sqrt{\dfrac{5a^2}{4}}\)
Chiều cao chóp cụt :\(\sqrt{\dfrac{3a^2}{4}}\)
Khẳng định nào sau đây là sai?
Các hình chóp sau đây luôn có các đỉnh nằm trên một mặt cầu:
A. Hình chóp tam giác B. Hình chóp ngũ giác đều
C. Hình chóp tứ giác D. Hình chóp đều n-giác.
Chọn C.
Điều kiện để hình chóp nội tiếp được trong một mặt cầu là đáy của nó nội tiếp trong một đường tròn. Một tứ giác bất kì chưa chắc nội tiếp trong một đường tròn.
Chọn C vì điều kiện để hình chóp nội tiếp được trong một mặt cầu là đáy của nó nội tiếp trong một đường tròn. Một tứ giác bất kì chưa chắc nội tiếp trong một đường tròn.
Cho hình chóp cụt đều có đáy là hình vuông, các cạnh đáy là a và b. Biết diện tích xung quanh bằng tổng diện tích hai đáy, tính chiều cao của hình chóp cụt đều.
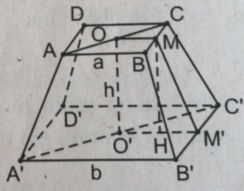
Xét hình chóp cụt đều ABCD.A'B'C'D' như hình bs.19.
Gọi M, M' thứ tự là trung điểm của BC, B'C'. Khi đó MM' là đường cao của hình thang cân BCC'B'.
Do đó diện tích xung quanh của hình chóp cụt đều là:
S x q = 4.(a+b)/2.MM′=(2a+2b).MM′
Từ giả thiết ta có:
(2a+2b).MM′=
a
2
+
b
2
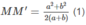
Dễ thấy OM // O'M' nên OM và O'M' xác định mặt phẳng (OMM'O'). Trong mặt phẳng (OMM'O'), kẻ MH ⊥ O'M'. Khi đó: HM' = O'M' – O'H = (b−a)/2
Trong tam giác vuông MHM' ta có: M M ' 2 = M H 2 + H M ' 2 = h + b - a / 2 2 (2)
Từ (1) và (2) suy ra :
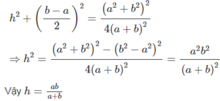
Cho hình chóp cụt đều có đáy là hình vuông, các cạnh đáy là a và b. Biết diện tích xung quanh bằng tổng diện tích hay đáy, tính chiều cao của hình chóp cụt đều.
Xét hình chóp cụt đều ABCD.AB'C'D'
Gọi M ,M' thứ tự là trung điểm của BC , B'C' . Khi đó MM' là đường cao của hình thang cân BCC'B' . Do đó diện tích xung quanh của hình chóp cụt đều là :
\(S_{xq}=4.\dfrac{a+b}{2}.MM'=\left(2a+2b\right).MM'\)
Từ giả thiết , ta có :
\(\left(2a+2b\right).MM'=a^2+b^2hayMM'=\dfrac{a^2+b^2}{2\left(a+b\right)}\left(1\right)\)
Dễ thấy OM // O'M' nên OM và O'M' xác định mặt phẳng (OMM'O') . Trong mặt phẳng (OMM'O') , kẻ MH \(\perp\) O'M' . Khi đó : \(HM'=O'M'-O'H=\dfrac{b-a}{2}\)
Trong tam giác vuông MHM' ta có :
\(MM'^2=MH^2+HM'^2=h^2+\left(\dfrac{b-a}{2}\right)^2\left(2\right)\)
Từ (1) và (2) suy ra :
\(h^2+\left(\dfrac{b-a}{2}\right)^2=\dfrac{\left(a^2+b^2\right)^2}{4\left(a+b\right)^2}\)
\(\Rightarrow h^2=\dfrac{\left(a^2+b^2\right)^2-\left(b^2-a^2\right)^2}{4\left(a+b\right)^2}=\dfrac{a^2b^2}{\left(a+b\right)^2}\)
Vậy \(h=\dfrac{ab}{a+b}\)
Trong các phát biểu sau, phát biểu nào đúng?
a) Hình chóp đều S.ABCD có đáy là hình bình hành.
b) Hình chóp đều S.ABCD có đáy là hình thoi, chân đường cao hình chóp là giao điểm của 2 đường chéo hình thoi.
c) Hình chóp đều S.ABCD có đáy là hình vuông, chân đường cao hình chóp là giao điểm của 2 đường chéo hình vuông.
d) Hình chóp đều S.ABCD có đáy là hình vuông, các mặt bên là các tam giác đều chung đỉnh S.