Giải bất phương trình f'(x) < 0 với f ( x ) = - 2 x 4 + 4 x 2 + 1
A. - 1 < x < 0 x > 1
B. -1 < x < 0
C. x > 1
D. x < 0
cho hàm số \(f\left(x\right)=x^3-3x^2+2\)
a, giải bất phương trình \(f'\left(x\right)\le0\)
b, giải phương trình \(f'=\left(x^2-3x+2\right)=0\)
c, đặt \(g\left(x\right)=f\left(1-2x\right)+x^2-x+2022\) giải bất phương trình\(g'\left(x\right)\ge0\)
\(a,f'\left(x\right)=3x^2-6x\\ f'\left(x\right)\le0\Leftrightarrow3x^2-6x\le0\\ \Leftrightarrow3x\left(x-2\right)\le0\Leftrightarrow0\le x\le2\)
Lời giải:
a. $f'(x)\leq 0$
$\Leftrightarrow 3x^2-6x\leq 0$
$\Leftrightarrow x(x-2)\leq 0$
$\Leftrightarrow 0\leq x\leq 2$
b.
$f'(x)=x^2-3x+2=0$
$\Leftrightarrow 3x^2-6x=x^2-3x+2=0$
$\Leftrightarrow 3x(x-2)=(x-1)(x-2)=0$
$\Leftrightarrow x-2=0$
$\Leftrightarrow x=2$
c.
$g(x)=f(1-2x)+x^2-x+2022$
$g'(x)=(1-2x)'f(1-2x)'_{1-2x}+2x-1$
$=-2[3(1-2x)^2-6(1-2x)]+2x-1$
$=-24x^2+2x+5$
$g'(x)\geq 0$
$\Leftrightarrow -24x^2+2x+5\geq 0$
$\Leftrightarrow (5-12x)(2x-1)\geq 0$
$\Leftrightarrow \frac{-5}{12}\leq x\leq \frac{1}{2}$
giúp mình với ạ hicc xét dấu biểu thức sau
a. f(x)= (x-3)(4-x)
b. f(x)= -x^2-5x+6
giải bất phương trình
a. x^2 + x - 2 = 0
b. (x-1)(x^2+3x+2)<= 2
tìm m để phương trình sau vô nghiệm x^2+(m+2)x+9/4=0
a, \(Chof\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\)
- Lập bảng xét dấu :
Vậy \(\left\{{}\begin{matrix}f\left(x\right)>0\Leftrightarrow x\in\left(3;4\right)\\f\left(x\right)< 0\Leftrightarrow x\in\left(-\infty;3\right)\cup\left(4;+\infty\right)\\f\left(x\right)=0\Leftrightarrow x\in\left\{3;4\right\}\end{matrix}\right.\)
b, \(f\left(x\right)=\left(x-1\right)\left(x+6\right)\)
( Làm tương tự câu a )
Giải bất phương trình: 2 x f ' ( x ) ≥ 0 với f ( x ) = x + x 2 + 1
A. x ≥ 1 3
B. x > 1 3
C. x < 1 3
D. x ≥ 2 3
- TXĐ: D = R
- Ta có:
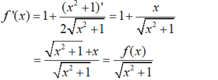
- Mặt khác:
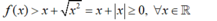
- Nên:
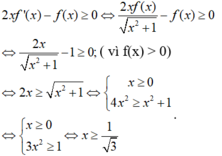
Chọn A.
Giải bất phương trình f'(x) < 0 với f ( x ) = - 2 x 4 + 4 x 2 + 1
A. - 1 < x < 0 x > 1
B. -1 < x < 0
C. x > 1
D. x < 0
Giải bất phương trình f ' ( x ) ≥ 0 với f ( x ) = 2 x 3 - 3 x 2 + 1
A. x ≤ 0 x ≥ 1
B. x ≤ 1
C. x ≥ 0
D. 0 ≤ x ≤ 1
Giải bất phương trình f ' ( x ) ≥ 0 với f ( x ) = 2 x 3 − 3 x 2 + 1
A. x ≤ 0 h o ặ c x ≥ 1
B. x ≤ 1
C. x ≥ 0
D. 0 ≤ x ≤ 1
Chọn A
Ta có: f ' ( x ) = 6 x 2 − 6 x
Để
f ' ( x ) ≥ 0 ⇔ 6 x 2 − 6 x ≥ 0 ⇔ x ≤ 0 x ≥ 1
Câu 1 : Cho tam thức bậc hai f(x)=-x2+(m+2)x-4. Tìm các giá trị của tham số m để :
a) Phương trình f(x)=0 có hai nghiệm phân biệt
b) Tam thức f(x)<0 với mọi x
Câu 2 : Cho bất phương trình 2x2+(m-1)x+1-m >0
a) Giải bất phương trình (1) với m=2
b) Tìm m để bất phương trình (1) nghiệm đúng với mọi giá trị của x
Câu 3 : Cho f(x)=(m-1)x2-2(m-1)x-1. Tìm m để bất phương trình f(x)>0 vô nghiệm.
Câu 1 : a/Δ Δ = (m+2)2 - 4(-1)(-4) = m2 +2m -12
ycbt <=> Δ > 0 <=> m2 +2m-12 > 0
<=> m < -1-\(\sqrt{13}\) ; m > -1+\(\sqrt{13}\)
Vậy giá trị cần tìm m ∈ (-∞; -1-\(\sqrt{13}\) ) U (-1+\(\sqrt{13}\) ; +∞)
b/ Δ = m2 +2m-12
ycbt <=> Δ < 0 <=> m2 +2m-12 < 0
<=> -1-\(\sqrt{13}\)<m< -1+\(\sqrt{13}\)
Câu 2 .
a/ Thay m=2 vào bpt ta được : 2x2+(2-1)x+1-2 >0
<=> 2x2 + x -1 > 0 <=> x < -1 ; x > \(\frac{1}{2}\)
Cho hàm số \(f\left(x\right)=x^2-3x+4\) . Giải bất phương trình \(f\left(x-x^2\right)\ge0\)
Cho hàm số \(f\left(x\right)=x^2-3x+4\). Giải bất phương trình \(f\left(x-x^2\right)\ge0\)