Cho hình thang cân ABCD có AB// CD và AB = BC. Tìm khẳng định sai.
A. B A C ^ = A C B ^
B. A D B ^ = A B D ^
C. tam giác ABD cân tại A
D. B D C ^ = A C B ^
1.)Hình thang ABCD ( góc A =90 , AB//CD ). AB =10cm, AD =12cm , BC = 20 cm . Chu vi của hình thang bằng: A. 66cm . B. 68cm. C. 70cm . D. 72cm .
2)Khẳng định nào sau đây sai? Tồn tại hình thang ABCD ( AB//CD) ta có :
A)AB=2cm, BC=4cm ,C= 7 cm, AD= 3cm .
B)AB=1cm, BC=3cm, CD=5cm, AD=2cm .
C)AB=6cm, BC=2cm, CD=10cm, AD= 4cm .
D)AB= 1cm, BC=2cm, CD=9cm, AD= 5cm.
3)Hình thang ABCD có góc A= 100 độ , góc B = 60 độ. Các góc C và góc D sẽ bằng:
A) góc C=120 độ ; D=80 độ, B) góc C= 80 độ; góc D= 120 độ
C) góc C= 100 độ; góc D= 100 độ D) góc B=90 độ,...
4)Hình thang có tối đa bao nhiêu góc vuông? Góc nhọn? Góc tù? Trả lời theo thứ tự là:
A) 4, 3, 3 ; B) 3, 3, 3 ; C) 3, 2, 2 ; D) 4, 2, 2 .
5). Cho hình thang vuông ABCD (AB //CD) có góc A= 90 độ , CD= 2AB=BC . Số đo góc C sẽ bằng:
A) 60 độ ; B) 90 độ ; C) 120 độ ; D) 150 độ
6)Cho tam giác ABC . Cắt các cạnh AB , AC bằng ba đường thẳng (không qua A và ) cùng song song với BC . Số hình thang tạo thành là:
A) 5 ; B) 6 ; C) 7 ; D) 8
7) Hình thang vuông có một góc bằng 75 độ . Chọn câu sai? Các góc của hình thang lần lượt là:
A) 75 độ ; B) 90 độ ; C) 95 độ ; D) 105 độ
Cho hình chóp S. ABCD có đáy là hình thang (AB// CD). Tìm khẳng định sai?
A. Hình chóp có 4 mặt bên.
B. Giao tuyến của mặt phẳng (SAC) và (SBD) là SO. ( O là giao điểm của AC và BD).
C. Giao tuyến của mặt phẳng (SAD) và ( SBD) là SI ( I là giao điểm của AD và BC).
D. Giao tuyến của mặt phẳng (SAB) và (SAD) là đường trung bình của hình thang ABCD
Chọn D
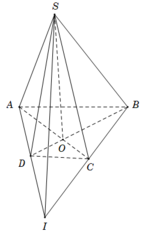
+Hình chóp S. ABCD có 4 mặt bên là (SAB); (SBC) ; (SCD) và (SAD): Do đó A đúng.
+ S là điểm chung thứ nhất của hai mặt phẳng (SAC) và (SBD)
là điểm chung thứ hai của hai mặt phẳng (SAC) và (SBD)
O ∈ A C ⊂ S A C ⇒ O ∈ S A C O ∈ B D ⊂ S B D ⇒ O ∈ S B D ⇒ O
=> giao tuyến của ( SAC) và (SBD) là SO.
Do đó B đúng.
+ Tương tự, ta có giao tuyến của mặt phẳng (SAD) và ( SBD) là SI ( I là giao điểm của AD và BC). Do đó C đúng.
+ giao tuyến của ( SAB) và (SAD) là SA mà SA không phải là đường trung bình của hình thang ABCD.
Do đó D sai.
Cho hình thang ABCD có AB // CD , hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD . Tìm khẳng định sai trong các khẳng định sau?
A. ABCD là hình thang cân
B. AC = BD
C. BC = AD
D. Tam giác AOD cân tại O.
* Ta có: OA = OB nên tam giác OAB cân tại O
* Do OC = OD nên tam giác OCD cân tại O
* vì OA = OB và OC = OD nên OA + OC = OB + OD
Hay AC = BD
Hình thang ABCD có hai đường chéo AC = BD nên đây là hình thang cân.
Suy ra: BC = AD và B A D ^ = A B C ^ ; A D C ^ = D C B ^
Chọn đáp án D
Mọi người xem đề bài này có sai không nha.
Bài 10: Cho hình thang cân ABCD có AB//CD và AB<CD,biết AD=BC.
a) C/m AB=BC. C/m DB là tia phân giác góc ADC
Cho hình thang ABCD có đáy là AB và CD. Gọi M và N lần lượt là trung điểm của AD và BC. Khẳng định nào sau đây sai?
A. M N → = M D → + C N → + D C → .
B. M N → = A B → − M D → + B N → .
C. M N → = 1 2 A B → + D C → .
D. M N → = 1 2 A D → + B C → .
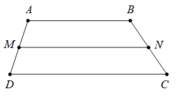
Vì M; N lần lượt là trung điểm của AD; BC
M A → + M D → = 0 → B N → + C N → = 0 → .
Dựa vào đáp án, ta có nhận xét sau:
A đúng, vì :
M D → + C N → + D C → = M N → = M D → + D C → + C N → = M C → + C N → = M N → .
B đúng, vì A B → − M D → + B N → = A B → + B N → − M D → = A N → − A M → = M N → .
C đúng, vì M N → = M A → + A B → + B N → và M N → = M D → + D C → + C N → .
Suy ra
2 M N → = M A → + M D → + A B → + D C → + B N → + C N → = 0 → + A B → + D C → + 0 → = A B → + D C →
⇒ M N → = 1 2 A D → + B C → .
D sai, vì theo phân tích ở đáp án C.
Chọn D.
Hình thang cân ABCD (AB// CD) có ∠ (A ) = 70 0 . Khẳng định nào dưới đây là đúng ?
A. ∠ (C ) = 110 0
B. ∠ (B ) = 110 0
C. ∠ (C ) = 70 0
D. ∠ (D ) = 70 0
Chọn A. ∠ (C ) = 110 0
Ta có : ∠ (A )+ ∠ (D )= 180 0 ( hai góc trong cùng phía)
=> ∠ (D )= 180 0 - ∠ (A )= 180 0 - 70 0 = 110 0
mà ∠ (C )= ∠ (D ) (tính chất hình thang cân ) => ∠ (C )= ∠ (D )= 110 0
Cho hình thang cân ABCD (AB // CD) có góc A= góc B= 60o, AB= 4,5 cm, AD = BC = 2cm. Tính CD và diện tích hình thang cân ABCD.
Cho hình thang cân ABCD (AB//CD) có A ^ = B ^ = 60 0 , AB = 4,5cm; AD = BC = 2 cm. Tính độ dài đáy CD và diện tích hình thang cân ABCD
Hạ CH và DK vuông góc với AB
Ta có:
A K = B H = 1 2 A D = 1 c m
Từ đó: CD = 2,5cm
C H = 3 c m
S A B C D = A B + C D . C D 2 = 7 3 2 c m 2

Cho hình thang cân ABCD (AB // CD) có hai đường chéo cắt nhau tại I, hai đường thẳng AD và BC cắt nhau ở K. Chọn khẳng định đúng:
A. KI là đường trung trực của hai đáy AB và CD.
B. KI là đường trung trực của đáy AB nhưng không là đường trung trực của CD.
C. KI là đường trung trực của đáy CD nhưng không là trung trực của AB.
D. KI không là đường trung trực của cả hai đáy AB và CD.
Đáp án cần chọn là: A
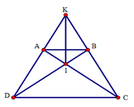
Xét tam giác ACD và tam giác BDC có:
+ AD = BC (do ABCD là hình thang cân)
+ AC = BD (do ABCD là hình thang cân)
+ CD là cạnh chung
Suy ra ΔACD = ΔBDC (c.c.c)
Suy ra A C D ^ = B D C ^ (cmt), suy ra tam giác ICD cân tại I. Do đó ID = IC (1)
Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K.
Do đó KC = KD (2)
Từ (1) và (2) suy ra KI là đường trung trực của CD (*).
Xét tam giác ADB và tam giác BCA có:
+ AD = BC (cmt)
+ AB là cạnh chung
+ AC = BD
Suy ra ΔADB = ΔBCA (c.c.c)
Suy ra A B D ^ = B A C ^
Xét tam giác IAB có A B D ^ = B A C ^ nên tam giác IAB cân tại I.
Do đó IA = IB (3)
Ta có KA = KD – AD; KB = KC – BC
Mà KD = KC, AD = BC, do đó KA = KB (4)
Từ (3) và (4) suy ra KI là đường trung trực của AB. (**)
Từ (*) và (**) suy ra KI là đường trung trực của hai đáy (đpcm)