Ta có A B → = − 1 ; 11 ,   A C → = − 7 ; 3 .

Suy ra A B → . A C → = − 1 . − 7 + 11.3 = 40.  

Chọn A.

Ta có A B → = − 1 ; 11 ,   A C → = − 7 ; 3 .

Suy ra   A B → . A C → = − 1 . − 7 + 11.3 = 40.

Chọn A.

Chọn D

\(\left\{{}\begin{matrix}x_B=\dfrac{x_A+x_C}{2}\\y_B=\dfrac{y_A+y_C}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1+x_C=4\\3+y_C=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_C=3\\y_C=-5\end{matrix}\right.\)

Ta có M ∈ O x  nên M(x;O) và  M A → = − 4 − x ; 0 M B → = − 5 − x ; 0 M C → = 3 − x ; 0 ⇒ M A → + M B → + M C → = − 6 − 3 x ; 0 .

Do M A → + M B → + M C → = 0 →  nên − 6 − 3 x = 0 ⇔ x = − 2 ⇒ M − 2 ; 0 .  

Chọn A.

\(\left\{{}\begin{matrix}x_G=\dfrac{-1+\left(-2\right)+4}{3}=\dfrac{1}{3}\\y_G=\dfrac{1+3+\left(-5\right)}{3}=-\dfrac{1}{3}\end{matrix}\right.\)

a: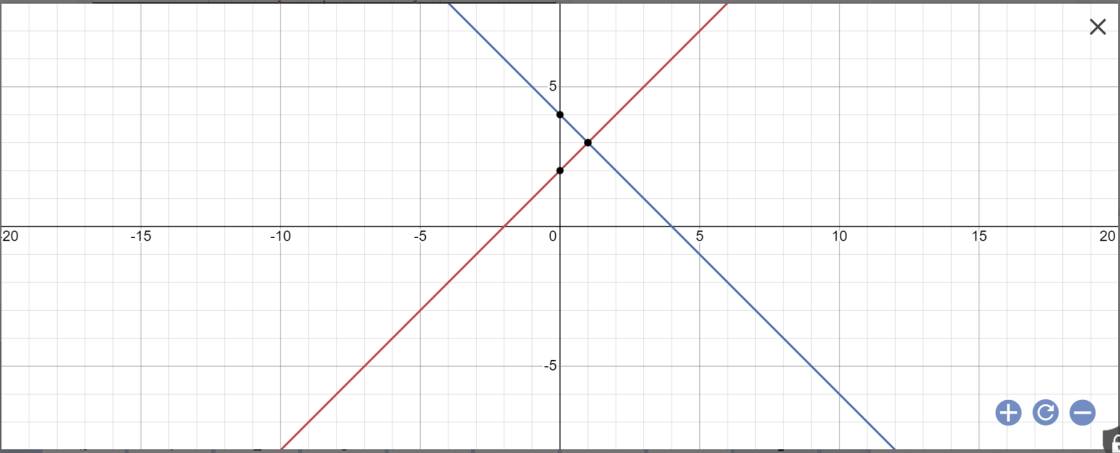 

b: Tọa độ giao điểm của (d1) và (d2) là:

\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)

Thay x=1 và y=3 vào (d3), ta được:

\(1\cdot m+m=3\)

=>2m=3

=>\(m=\dfrac{3}{2}\)

Giả sử A = (x; y). Khi đó

Vậy A = (5; 1)

Giả sử A = (x; y). Khi đó

Vậy A = (1; 3)