Tìm m để hàm số f x = x x - m xác định trên khoảng (0;5).
A. 0 < m < 5
B. m ≤ 0
C. m ≥ 5
D. m ≤ 0 hoặc m ≥ 5
Những câu hỏi liên quan
Cho hàm số yf(x) xác định trên R{0}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau:Tìm tất cả các giá trị của tham số thực m để phương trình f(x) -m0 A.
m
∈
3
;
+
∞
B.
m
∈
−
∞
;
1
∪
3
;
+...
Đọc tiếp
Cho hàm số y=f(x) xác định trên R\{0}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau:
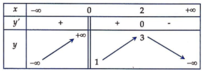
Tìm tất cả các giá trị của tham số thực m để phương trình f(x) -m=0
A. m ∈ 3 ; + ∞
B. m ∈ − ∞ ; 1 ∪ 3 ; + ∞
C. m ∈ 3 ; + ∞
D. m ∈ − ∞ ; 1 ∪ 3 ; + ∞
Đáp án A.
Ta có f x − m = 0 ⇔ f x = m . Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f x và đường thẳng y = m .Do đó để phương trình đã cho có nghiệm duy nhất thì đường thẳng y = m phải cắt đồ thị hàm số y = f x tại một điểm duy nhất. Khi đó m ∈ 3 ; + ∞ .
Đúng 0
Bình luận (0)
Cho hàm số yf(x) xác định trên
ℝ
0
, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau: Tìm tất cả các giá trị của tham số thực m để phương trình f(x)-m0 có nghiệm duy nhất. A.
m
∈
3
;
+
∞
B.
m
∈
−
∞
;...
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ \ 0 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau:
Tìm tất cả các giá trị của tham số thực m để phương trình f(x)-m=0 có nghiệm duy nhất.
A. m ∈ 3 ; + ∞
B. m ∈ − ∞ ; 1 ∪ 3 ; + ∞
C. m ∈ 3 ; + ∞
D. m ∈ − ∞ ; 1 ∪ 3 ; + ∞
Cho hàm số y f(x) xác định trên tập hợp
ℝ
0
liên tục trên khoảng xác định có bảng biến thiên như sau. Tìm tất cả các giá trị của m để phương trình f(x) m có hai nghiệm thực phân biệt. A. m 2 B. m 1 C. m 2 hoặc m 1 D.
m
≤
1
hoặc m 2
Đọc tiếp
Cho hàm số y = f(x) xác định trên tập hợp ℝ \ 0 liên tục trên khoảng xác định có bảng biến thiên như sau. Tìm tất cả các giá trị của m để phương trình f(x) = m có hai nghiệm thực phân biệt.
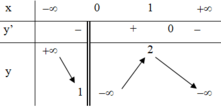
A. m = 2
B. m < 1
C. m = 2 hoặc m < 1
D. m ≤ 1 hoặc m = 2
Đáp án D
Từ bảng biến thiên ta thấy với m = 2 hoặc m ≤ 1 thì đồ thị hàm số y = f(x) cắt đường thẳng y = m tại 2 điểm phân biệt hay phương trình f(x) = m có 2 nghiệm phân biệt.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) xác định trên
R
/
2
, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sauTìm tập hợp các giá trị của tham số m để phương trình 2f(x)-m0 có hai nghiệm. A.
(
-
∞
;
-
2
)
∪
(
6
;
+
∞
)
B.
(
-
∞
;
-
6...
Đọc tiếp
Cho hàm số y=f(x) xác định trên R / 2 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau
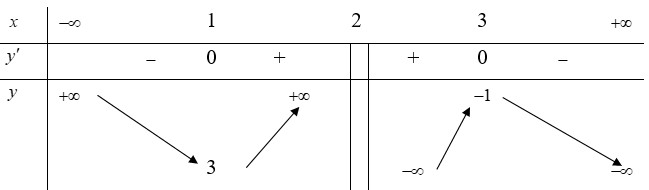
Tìm tập hợp các giá trị của tham số m để phương trình 2f(x)-m=0 có hai nghiệm.
A. ( - ∞ ; - 2 ) ∪ ( 6 ; + ∞ )
B. ( - ∞ ; - 6 ) ∪ ( - 2 ; + ∞ )
C. ( 2 ; 6 )
D. ( - 6 ; - 2 )
Cho hàm số yf(x) xác định và liên tục trên các khoảng
(
-
∞
;
0
)
,
(
0
;
+
∞
)
và có bảng biến thiên như sauTìm tất cả các giá trị thực của m để đường thẳng ym cắt đổ thị hàm số yf(x) tại 3 điểm phân biệt A.
-
4
≤
m
0
B.
-
4
m
0...
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên các khoảng ( - ∞ ; 0 ) , ( 0 ; + ∞ ) và có bảng biến thiên như sau
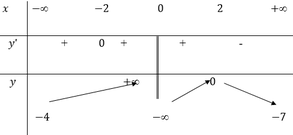
Tìm tất cả các giá trị thực của m để đường thẳng y=m cắt đổ thị hàm số y=f(x) tại 3 điểm phân biệt
A. - 4 ≤ m < 0
B. - 4 < m < 0
C. - 7 < m < 0
D. - 4 < m ≤ 0
Tìm m để hàm số
y
x
−
2
m
+
3
x
−
m
+
3
x
−
1
−
x
+
m
+
5
xác định trên k...
Đọc tiếp
Tìm m để hàm số y = x − 2 m + 3 x − m + 3 x − 1 − x + m + 5 xác định trên khoảng (0; 1)
A. m ∈ 1 ; 3 2
B. m ∈ − 3 ; 0
C. m ∈ − 3 ; 0 ∪ 0 ; 1
D. m ∈ − 4 ; 0 ∪ 1 ; 3 2
Cho hàm số xác định trên
ℝ
0
,
liên tục trên mỗi khoảng xác định và có bảng biến thiên như sauTìm tất cả các giá trị thực của tham số m để phương trình f (x) m có hai nghiệm thực phân biệt. A.
m
∈
3
;
+
∞
B.
m
∈
−
∞...
Đọc tiếp
Cho hàm số xác định trên ℝ \ 0 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau
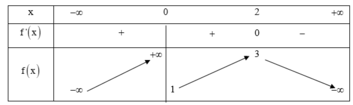
Tìm tất cả các giá trị thực của tham số m để phương trình f (x) = m có hai nghiệm thực phân biệt.
A. m ∈ 3 ; + ∞
B. m ∈ − ∞ ; 1 ∪ 3
C. m ∈ 3 ; + ∞
D. m ∈ − ∞ ; 1 ∪ 3 ; + ∞
Tìm tất cả các giá trị của tham số m để hàm số
y
1
m
log
3
2
x
-
4
log
3
x
+
...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số y = 1 m log 3 2 x - 4 log 3 x + m + 3 xác định trên khoảng ( 0 ; + ∞ )
A . m ∈ - ∞ ; - 4 ∪ ( 1 ; + ∞ )
B . m ∈ ( 1 ; + ∞ )
A . m ∈ - ∞ ; - 4 ∪ ( 1 ; + ∞ )
C . m ∈ ( - ∞ ; - 4 )
Chọn A
Cách 1
Điều kiện: x > 0
Hàm số xác định khi:
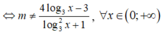
Để hàm số xác định trên
(
0
;
+
∞
)
thì phương trình 
Xét hàm số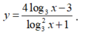 
Đặt 
khi đó ta có
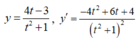
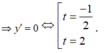
Ta có BBT:
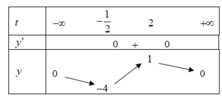
Để hàm số xác định trên 
Cách 2:
Đề hàm số xác định trên khoảng 
thi phương trình 
vô nghiệm.
TH1: m = 0 thì PT trở thành 
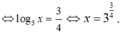
Vậy m = 0 không thỏa mãn.
TH2:
m
≠
0 thì để PT vô nghiệm 
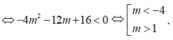
Để hàm số xác định trên 
Đúng 0
Bình luận (0)
Cho hàm số y f(x) xác định trên R{-1}, liên tục trên từng khoảng xác định và có bảng biến thiên như dưới đây:Tìm tập hợp tất cả các số thực của m để phương trình f(x)m có nghiệm thực duy nhất
A
.
(
0
;
+
∞
)
∪
-
1
B
.
(
0
;
+
∞
)
C
.
[
0
;...
Đọc tiếp
Cho hàm số y = f(x) xác định trên R\{-1}, liên tục trên từng khoảng xác định và có bảng biến thiên như dưới đây:
Tìm tập hợp tất cả các số thực của m để phương trình f(x)=m có nghiệm thực duy nhất
A . ( 0 ; + ∞ ) ∪ - 1
B . ( 0 ; + ∞ )
C . [ 0 ; + ∞ )
D . [ 0 ; + ∞ ) ∪ - 1
Cho hàm số y = (3 – m)x2a) Tìm điều kiện của m để hàm số trên được xác định.b) Xác định m để hàm số đồng biến với mọi x < 0.c) Xác định m để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0.
a, ĐKXĐ để hàm được xác định : \(3-m\ne0\)
\(\Leftrightarrow m\ne3\)
b, - Với x < 0 để hàm số đồng biến thì : \(3-m< 0\)
\(\Leftrightarrow m>3\)
Vậy ...
c, - Để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0
\(\Leftrightarrow a>0\)
\(\Leftrightarrow3-m>0\)
\(\Leftrightarrow m< 3\)
Vậy ...
Đúng 2
Bình luận (0)
a) Để hàm số \(y=\left(3-m\right)x^2\) được xác định thì \(3-m\ne0\)
hay \(m\ne3\)
b) Để hàm số \(y=\left(3-m\right)x^2\) đồng biến với mọi x<0 thì \(3-m< 0\)
\(\Leftrightarrow m>3\)
c) Để y=0 là giá trị nhỏ nhất của hàm số tại x=0 thì 3-m>0
hay m<3
Đúng 2
Bình luận (0)