Một hình trụ tròn xoay bán kính đáy bằng R, trục O ' O = R 6 . Một đoạn thẳng A B = R 2 với A ∈ O và B ∈ O . Tính góc giữa AB và trục hình trụ.
A. 30 o
B. 45 o
C. 60 o
D. 75 o
Một hình trụ tròn xoay bán kính đáy bằng R, trục O'O = R 6 . Một đoạn thẳng AB = R 2 với A ∈ (O) và B ∈ (O'). Tính góc giữa AB và trục hình trụ.
A. 30 ∘
B. 45 ∘
A. 60 ∘
D. 75 ∘
Một hình trụ tròn xoay bán kính R=1. Trên hai đường tròn đáy (O) và (O’). Lấy A và B sao cho AB=2. Góc giữa AB và trục OO’ bằng
30
°
. Xét hai khẳng định sau:
![]()
![]()
![]()
![]()
Một hình trụ có các đáy là hai hình tròn tâm O và O’ bán kính r và có đường cao h = r 2 . Gọi A là một điểm trên đường tròn tâm O và B là một điểm trên đường tròn tâm O’ sao cho OA vuông góc với O’B. Chứng minh rằng ( α ) tiếp xúc với mặt trụ trục OO’ có bán kính bằng r 2 2 dọc theo một đường sinh.
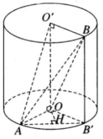
Đường tròn tâm O có bán kính bằng r 2 2 tiếp xúc với AB’ tại H là trung điểm của AB’. Do đó mặt phẳng ( α ) song song với trục OO’ chứa tiếp tuyến của đường tròn đáy, nên ( α ) tiếp xúc với mặt trụ dọc theo một đường sinh, với mặt trụ có trục OO’ và có bán kính đáy bằng r 2 2
Hình trụ tròn xoay có bán kính đáy bằng r, có chiều cao bằng 2r và có trục là OO’. Cắt hình trụ bởi một mặt phẳng song song với trục OO’ và cách trục một khoảng bằng r/2. Tính diện tích thiết diện thu được.
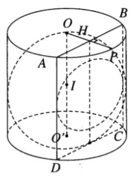
Trên mặt đáy tâm O ta gọi H là trung điểm của bán kính OP. Qua H kẻ dây cung AB ⊥ OP và nằm trong đáy (O; r). Các đường sinh AD và BC cùng với các dây cung AB và DC (thuộc đáy (O’, r)) xác định cho ta thiết diện cần tìm là một hình chữ nhật. Gọi S là diện tích hình chữ nhật này, ta có: SABCD= AB.AD trong đó AD = 2r còn AB = 2AH. Vì H là trung điểm của OP nên ta tính được AB = r 3 . Vậy S ABCD = 2 r 2 3
Cho hình trụ có chiều cao h = 5, bán kính đáy r = 2. Một đoạn thẳng có chiều dài bằng 6 và có hai đầu mút nằm trên hai đường tròn đáy. Tính khoảng cách d từ đoạn thẳng đó đến trục của hình trụ.
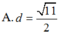
![]()
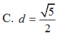
![]()
Cho hình trụ có chiều cao h = 5, bán kính đáy r = 2. Một đoạn thẳng có chiều dài bằng 6 và có hai đầu mút nằm trên hai đường tròn đáy. Tính khoảng cách d từ đoạn thẳng đó đến trục của hình trụ.
A. d = 11 2
B. d = 2
C. d = 5 2
D. d = 4 2
Một hình trụ có bán kính r và chiều cao h = r √3
Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng 30 o .Tính khoảng cách giữa đường thẳng AB và trục của hình trụ.
Cho hình trụ có hai đáy là hai hình tròn (O) và (O') chiều cao R 3 và bán kính đáy R. Một hình nón có đỉnh O’ và đáy là hình tròn (O;R). Tỷ lệ diện tích xung quanh của hình trụ và hình nón bằng
A. 3
B. 2
C. 2
D. 3
Hình trụ tròn xoay có bán kính đáy bằng r, có chiều cao bằng 2r và có trục là OO'
a) Chứng minh rằng mặt cầu đường kính OO' tiếp xúc với hai mặt đáy của hình trụ và tiếp xúc với tất cả các đường sinh của mặt trụ
b) Cắt hình trụ bởi một mặt phẳng song song với trục OO' và cách trục một khoảng bằng \(\dfrac{r}{2}\). Tính diện tích thiết diện thu được
c) Thiết diện nói trên cắt mặt cầu đường kính OO' theo thiết diện là một đường tròn. Tính bán kính của đường tròn đó