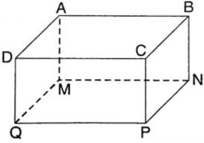
Cho hình hộp chữ nhật ABCD.MNPQ. Chứng minh rằng ( AMQD ) ⊥ ( CPQD )
Cho hình hộp chữ nhật ABCD.MNPQ có AB=15cm, AD = 20 cm và AM = 12cm Tính thể
tích hình hộp chữ nhật ABCD.MNPQ
Thể tích hình hộp chữ nhật ABCD.MNPQ được tính bằng tích diện tích đáy ABCD và chiều cao h:
$$V = S_{ABCD} \times h$$
Ta có $S_{ABCD} = AB \times AD = 15 \times 20 = 300$ (cm$^2$)
Để tính chiều cao h, ta cần tìm độ dài MP. Ta có:
$$MP = \sqrt{AM^2 + AP^2} = \sqrt{12^2 + 15^2} = \sqrt{369}$$
Vậy $h = MP = \sqrt{369}$ (cm)
Do đó, thể tích hình hộp ABCD.MNPQ là:
$$V = S_{ABCD} \times h = 300 \times \sqrt{369} \approx 5587.6 \text{ (cm}^3\text{)}$$
Vậy thể tích hình hộp chữ nhật ABCD.MNPQ là khoảng 5587.6 cm$^3$.
Cho hình hộp chữ nhật ABCD.MNPQ có chiều dài A B = 22 c m ; chiều rộng B C = 14 c m ; chiều cao A M = 5 c m . Thể tích hình hộp chữ nhật ABCD.MNPQ là:
A. 1 540 c m 3
B. 770 c m 3
C. 2 310 c m 3
D. 180 c m 3
Cho hình hộp chữ nhật ABCD.MNPQ có AB :AD : AM = 3:4:6 và AP= \(\sqrt{3075,01}cm\)
a/ Chứng minh ACPM là hình chữ nhật. Tính diện tích tứ giác ACPM
b/ Tính thể tích hình hộp chữ nhật ABCD.MNPQ
Cho hình hộp chữ nhật ABCD.MNPQ có chiều dài AB = 90cm, chiều cao AM = 70cm và diện tích xung quanh bằng 21000 c m 2 . Chiều rộng BC của hình hộp chữ nhật là:
A. 60cm
B. 80cm
C. 100cm
D. 120cm
Hãy kể tên những cạnh bằng nhau của hình hộp chữ nhật ABCD.MNPQ (h.72).
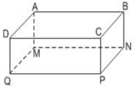
Trong hình hộp chữ nhật ABCD.MNPQ những cạnh bằng nhau là:
AB = CD = PQ = MN
AD = QM = PN = CB
DQ = AM = BN = CP
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 12cm, AD = 16cm, AA' = 25cm.
a) Chứng minh rằng các tứ giác ACCA', BDD'B' là những hình chữ nhật.
b) Chứng minh rằng AC'2 = AB2 + AD2 + AA'2.
c) Tính diện tích toàn phần và thể tích của hình hộp chữ nhật.
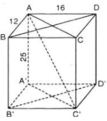
a) ABCD.A’B’C’D’ là hình hộp chữ nhật
⇒ AA’ // CC’, AA’ = CC’
⇒ AA’C’C là hình bình hành
Lại có : AA’ ⊥ (ABCD) ⇒ AA’ ⊥ AC ⇒ 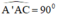
⇒ Hình bình hành AA’C’C là hình chữ nhật.
Chứng minh tương tự được tứ giác BDD'B' là những hình chữ nhật
b) Áp dụng định lý Pytago:
Trong tam giác vuông ACC’ ta có:
AC’2 = AC2 + CC’2 = AC2 + AA’2
Trong tam giác vuông ABC ta có:
AC2 = AB2 + BC2 = AB2 + AD2
Do đó: AC’2 =AB2 + AD2 + AA’2.
c) Hình hộp chữ nhật được xem như hình lăng trụ đứng.
Diện tích xung quanh:
Sxq = 2.(AB + AD).AA’
= 2.(12 + 16).25
= 1400 (cm2 )
Diện tích một đáy:
Sđ = AB.AD
= 12.16
= 192 (cm2 )
Diện tích toàn phần:
Stp = Sxq + 2Sđ
= 1400 + 2.192
= 1784 (cm2 )
Thể tích:
V = AB.AD.AA’
= 12.16.25
= 4800 (cm3 )
Hãy kể tên những cạnh bằng nhau của hình hộp chữ nhật ABCD.MNPQ( ét o ét)
Trong hình hộp chữ nhật ABCD.MNPQ những cạnh bằng nhau là:
AB = CD = PQ = MN
AD = QM = PN = CB
DQ = AM = BN = CP
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Chứng minh rằng:
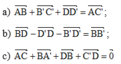
Cho hình hộp chữ nhật ABCD.MNPQ
a/ Đoạn thẳng AB vuông góc với mặt phẳng nào ?
b/ Mặt phẳng ( NPCB ) vuông góc với mặt phẳng nào? song song với mặt phẳng nào ?
c/ Biết AM= 10cm , NP = 8cm , AB = 6cm . Tính diện tích toàn phần hình hộp chữ nhật , thể tích hình hộp chữ nhật