cho a+b+c=0 và a≠0,b≠0,c≠0 tính M
M=a2/a2-b2-c2 +b2/b2-c2-a2 +c2/c2-a2-b2
Ta có: a+b+c=0
nên a+b=-c
Ta có: \(a^2-b^2-c^2\)
\(=a^2-\left(b^2+c^2\right)\)
\(=a^2-\left[\left(b+c\right)^2-2bc\right]\)
\(=a^2-\left(b+c\right)^2+2bc\)
\(=\left(a-b-c\right)\left(a+b+c\right)+2bc\)
\(=2bc\)
Ta có: \(b^2-c^2-a^2\)
\(=b^2-\left(c^2+a^2\right)\)
\(=b^2-\left[\left(c+a\right)^2-2ca\right]\)
\(=b^2-\left(c+a\right)^2+2ca\)
\(=\left(b-c-a\right)\left(b+c+a\right)+2ca\)
\(=2ac\)
Ta có: \(c^2-a^2-b^2\)
\(=c^2-\left(a^2+b^2\right)\)
\(=c^2-\left[\left(a+b\right)^2-2ab\right]\)
\(=c^2-\left(a+b\right)^2+2ab\)
\(=\left(c-a-b\right)\left(c+a+b\right)+2ab\)
\(=2ab\)
Ta có: \(M=\dfrac{a^2}{a^2-b^2-c^2}+\dfrac{b^2}{b^2-c^2-a^2}+\dfrac{c^2}{c^2-a^2-b^2}\)
\(=\dfrac{a^2}{2bc}+\dfrac{b^2}{2ac}+\dfrac{c^2}{2ab}\)
\(=\dfrac{a^3+b^3+c^3}{2abc}\)
Ta có: \(a^3+b^3+c^3\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ca-cb+c^2\right)-3ab\left(a+b\right)\)
\(=-3ab\left(a+b\right)\)
Thay \(a^3+b^3+c^3=-3ab\left(a+b\right)\) vào biểu thức \(=\dfrac{a^3+b^3+c^3}{2abc}\), ta được:
\(M=\dfrac{-3ab\left(a+b\right)}{2abc}=\dfrac{-3\left(a+b\right)}{2c}\)
\(=\dfrac{-3\cdot\left(-c\right)}{2c}=\dfrac{3c}{2c}=\dfrac{3}{2}\)
Vậy: \(M=\dfrac{3}{2}\)
Cho đường tròn (C) : x2+ y2-2ax – 2by + c= 0 (a2+ b2- c > 0) . Hỏi mệnh đề nào sau đây sai?
A. (C) có bán kính R= a 2 + b 2 - c .
B. (C) tiếp xúc với trục hoành khi và chỉ khi b2= R2.
C. (C) tiếp xúc với trục tung khi và chỉ khi a= R. .
D. (C) tiếp xúc với trục tung khi và chỉ khi b2= c.
Xét phương án C:
(C) tiếp xúc với trục Oy khi d ( I ; y ' O y ) = R ⇔ a = R .
Do đó đáp án (C) sai vì nếu a= -9 => R= -9 < 0 (vô lý)
Chọn C.
Rút gọn biểu thức M=\(\sqrt{a^4}\)-\(a\sqrt{a^2}\)-\(\dfrac{b}{2}\sqrt{4b^2}\)-b2 (a≤0; b≥0) ta được:
A.2b2 B.2a2 C.0 D.2(a2-b2)
\(M=a^2-a\left|a\right|-\dfrac{b}{2}\cdot2\left|b\right|-b^2\\ M=a^2+a^2-b^2-b^2\\ M=2\left(a^2-b^2\right)\\ D\)
Cho biểu thức:
M = a a 2 - b 2 + 1 + a a 2 - b 2 : b a - a 2 - b 2 với a > b > 0
c) Tìm điều kiện của a, b để M < 1.
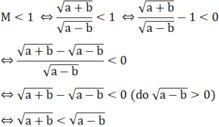
<=> a+b < a-b
<=> b < 0
Vô lí do a > b > 0
Vậy không tồn tại a, b sao cho M < 1
cho a,b,c khác 0 ; a+b+c=0 tính a=1/(a2+b2-c2)+1/(b2+c2-a2)+1/(a2+c2-b2)
Câu hỏi của Hattory Heiji - Toán lớp 8 - Học toán với OnlineMath
tvbobnokb' n
iai
ni;bv nn0
Các số thực a,b,c,x,y,z thỏa mãn a 2 + b 2 + c 2 - 2 a + 4 c + 4 = 0 và x 2 + y 2 + z 2 - 4 x + 4 y + 4 = 0 . Tìm GTLN của S = a - x 2 + b - y 2 + z - c 2 .
Trong mặt phẳng Oxy , đường thẳng d : a x + b y + c = 0 , a 2 + b 2 ≠ 0 . Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng d ?
A. n → = a ; - b
B. n → = b ; a
C. n → = b ; - a
D. n → = a ; b
Chọn D.
Ta có một vecto pháp tuyến của đường thẳng d là n → = a ; b
Tìm mối liên hệ giữa a, b, c để phương trình b 2 + c 2 x 2 - 2 a c x + a 2 - b 2 = 0 có nghiệm.
Bài 3 Chứng minh rằng với a, b, c, x, y, z (trong đó xyz 6= 0) thỏa mãn (a2 + b2 + c2)(x2 + y2 + z2) = (ax + by + cz)2
thì a/x =b/y =c/z.
Gọi a; b; c là ba cạnh của một tam giác. Chứng minh rằng phương trình sau vô nghiệm: c 2 x 2 + a 2 - b 2 - c 2 x + b 2 = 0.
c 2 x 2 + a 2 - b 2 - c 2 x + b 2 = 0.
Δ = a 2 - b 2 - c 2 2 - 4 b 2 c 2
= a 2 - b 2 - c 2 2 - 2 b c 2
= ( a 2 - b 2 - c 2 + 2bc)( a 2 - b 2 - c 2 - 2bc)
= [ a 2 - b - c 2 ][ a 2 - b + c 2 ]
= (a + b – c)(a – b + c)(a + b + c)(a – b – c)
Vì a; b; c là độ dài ba cạnh của một tam giác, dựa vào tính chất bất đẳng thức tam giác, ta có: |b – c| < a < b + c.
Do đó a + b + c > 0; a + b – c > 0; a – b + c > 0 còn a – b – c < 0.
Suy ra Δ < 0. Vậy phương trình đã cho vô nghiệm.
