Trong mặt phẳng Oxy phép đối xứng tâm I biến M(6; -9) thành M'(3;7). Tọa độ của tâm đối xứng I là:
A. I(-3/2; -8)
B. (-3;16)
C. (9/2; -1)
D. I(-3/2; -1)
Những câu hỏi liên quan
Trong mặt phẳng Oxy cho điểm M(-5;9). Phép đối xứng tâm I(2; -6) biến M thành M’ thì tọa độ M’ là.
A. M'(9;-15)
B. M'(9;-3)
C.M'(9;-21)
D. M'(1;-3)
Trong mặt phẳng Oxy cho điểm M(2;-6) và điểm I(1;4). Phép đối xứng tâm I biến M thành M’ thì tọa độ M’ là:
A. M’(0;14)
B. M’(14;0)
C. M’(-3/2;-2)
D. M’(-1/2;5)
Trong mặt phẳng Oxy cho điểm I(2; -5). Phép đối xứng tâm I biến M(x; y) thành M'(3; 7). Tọa độ của M là:
A. M(5/2;1)
B. M(7;-3)
C. M(-1;-12)
D. M(1;-17)
Trong mặt phẳng Oxy, phép đối xứng tâm O biến điểm M(2,-3) thành điểm nào sau đây.
A. M'(2;3)
B. M'(-2;3)
C. M'(2;-3)
D. M'(3;-2)
Trong mặt phẳng Oxy, phép đối xứng tâm O biến điểm M(2;-3) thành điểm nào sau đây.
A. M'(2; 3)
B. M'(-2; 3)
C. M'(2; -3)
D. M'(3; -2)
Trong mặt phẳng Oxy cho điểm M(-3;7). Phép đối xứng tâm O biến M thành M’ thì tọa độ M’ là:
A. M’(-3;-7)
B. M’(3;-7)
C. M’(7;-3)
D. M’(7;3)
Phép đối xứng tâm O biến M(x;y) thành M’(-x;-y).
Chọn đáp án B
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình
x
2
+
y
2
+
2
x
-
6
y
+
6
0
; điểm I(1;2). Phép đối xứng tâm I biến (C) thành (C’) có phương trình: A.
x
2
+
y
2...
Đọc tiếp
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x 2 + y 2 + 2 x - 6 y + 6 = 0 ; điểm I(1;2). Phép đối xứng tâm I biến (C) thành (C’) có phương trình:
A. x 2 + y 2 - 6 x - 2 y + 6 = 0
B. x 2 + y 2 - 2 x - 6 y + 6 = 0
C. x 2 + y 2 + 6 x - 2 y - 6 = 0
D. x 2 + y 2 - 6 x + 2 y + 6 = 0
Phép đối xứng tâm I(1; 2) biến M(x; y) thành M’(x’; y’) thì:
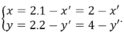
Thay vào phương trình (C) ta được:
2 - x ' 2 + 4 - y ' 2 + 2 ( 2 - x ' ) - 6 ( 4 - y ' ) + 6 = 0
⇒ x ' 2 + y ' 2 - 6 x ' - 2 y ' + 6 = 0 hay x 2 + y 2 - 6 x - 2 y + 6 = 0
Đáp án A
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, thực hiện liên tiếp phép quay tâm O góc quay - 45 o và phép đối xứng tâm O thì điểm M(1;1) biến thành điểm M’’ có tọa độ là:
A. (-1;0)
B. (√2;0)
C. (√2;-√2)
D. (-√2;0)
+) Phép quay tâm O góc quay − 45 ° biến điểm M(x; y) thành điểm M’(x’;y’) với biểu thức tọa độ là:
Với M(1; 1) suy ra tọa độ điểm M’ là x ' = x cos − 45 ° − y sin − 45 ° y ' = x sin − 45 ° + y cos − 45 ° ⇔ x ' = 2 2 x + 2 2 y y ' = − 2 2 x + 2 2 y
+) Phép đối xứng tâm O biến điểm M’ thành M’’ x ' = 2 2 .1 + 2 2 .1 = 2 y ' = − 2 2 .1 + 2 2 .1 = 0 ⇒ M ' 2 ; 0
Suy ra tọa độ M ' ' − 2 ; 0
Đáp án D
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho đường thẳng d:x-2y+20; d:x-2y-80 Phép đối xứng tâm biến d thành d và biến trục Ox thành chính nó có tâm I là: A. (0;-3) B. (0;3) C. (-3;0) D. (3,0)
Đọc tiếp
Trong mặt phẳng Oxy, cho đường thẳng d:x-2y+2=0; d':x-2y-8=0 Phép đối xứng tâm biến d thành d' và biến trục Ox thành chính nó có tâm I là:
A. (0;-3)
B. (0;3)
C. (-3;0)
D. (3,0)
