Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có tâm I. Gọi V, V 1 lần lượt là thể tích của khối hộp A B C D . A ' B ' C ' D ' và khối chóp I.ABCD. Tính tỉ số k = V 1 V
A. k = 1 6
B. k = 1 3
C. k = 1 8
D. k = 1 12
Cho hình hộp chữ nhật A B C D . A , B , C , D , có tâm I. Gọi V , V 1 lần lượt là thể tích của khối hộp A B C D . A , B , C , D , và khối chóp I . A B C D Tính tỉ số k = V 1 V .
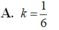
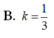
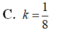
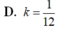
Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật. Tâm của mặt cầu (S) là:
A. Tâm của hình hộp chữ nhật
B. Tâm của một mặt bên của hình hộp chữ nhật
C. Trung điểm của một cạnh của hình hộp chữ nhật
D. Một đỉnh bất kì của hình hộp chữ nhật
Chọn A.
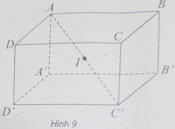
(h.9) Tâm của hình hộp chữ nhật cách đều 8 đỉnh của hình hộp nên tâm của mặt cầu (S) chính là tâm của hình hộp chữ nhật.
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có A B = a , A A ' = 2 a . Biết thể tích hình cầu ngoại tiếp tứ diện ABCD′ là 9 π 2 a 3 . Tính thể tích V của hình chữ nhật ABCD.A′B′C′D′.
A. 4 a 3
B. 4 a 3 3
C. 2 a 3
D. 2 a 3 3
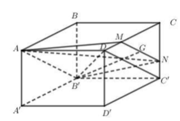
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = 3 a , A D = 4 a , A A ' = 4 a . Gọi G là trọng tâm tam giác CC 'D . Mặt phẳng chứa B'G và song song với C 'D chia khối hộp thành 2 phần. Gọi (H) là khối đa diện chứa C . Tính tỉ số V H V với V là thể tích khối hộp đã cho.
A. 19 54
B. 38 3
C. 23 4
D. 25 2
Phương pháp:
- Dựng mặt phẳng chứa B'G và song song với C'D.
- Xác định khối đa diện và tính thể tích bằng cách cộng trừ thể tích các khối đa diện đơn giản.
Cách giải:

Cho hình hộp chữ nhật ABCD.A' B' C' D' có các kích thước là AB=2, AD=3, AA'=4. Gọi (N) là hình nón có đỉnh là tâm của mặt ABB' A' và đường tròn đáy là đường tròn ngoại tiếp hình chữ nhật. Thể tích của khối nón (N) là
A. 5 π
B. 13 π 3
C. 8 π
D. 25 π 6
Cho hình hộp ABCD.A'B'C'D' có tâm O. Gọi I là tâm hình bình hành ABCD. Đặt \(\overrightarrow{AC'}=\overrightarrow{u},\overrightarrow{CA'}=\overrightarrow{v},\overrightarrow{BD'}=\overrightarrow{x},\overrightarrow{DB'}=\overrightarrow{y}\). Đẳng thức nào sau đây đúng/
A. \(2\overrightarrow{OI}=-\dfrac{1}{2}\left(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{x}+\overrightarrow{y}\right)\)
B. \(2\overrightarrow{OI}=-\dfrac{1}{4}\left(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{x}+\overrightarrow{y}\right)\)
C. \(2\overrightarrow{OI}=\dfrac{1}{4}\left(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{x}+\overrightarrow{y}\right)\)
D. \(2\overrightarrow{OI}=\dfrac{1}{2}\left(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{x}+\overrightarrow{y}\right)\)
Cho hình hộp ABCD.A'B'C'D' có tâm O. Gọi I là tâm hình bình hành ABCD. Đặt \(\overrightarrow{AC'}=\overrightarrow{u},\overrightarrow{CA'}=\overrightarrow{v},\overrightarrow{BD'}=\overrightarrow{x},\overrightarrow{DB'}=\overrightarrow{y}\). Đẳng thức nào sau đây đúng/
A. \(2\overrightarrow{OI}=-\dfrac{1}{2}\left(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{x}+\overrightarrow{y}\right)\)
B. \(2\overrightarrow{OI}=-\dfrac{1}{4}\left(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{x}+\overrightarrow{y}\right)\)
C. \(2\overrightarrow{OI}=\dfrac{1}{4}\left(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{x}+\overrightarrow{y}\right)\)
D. \(2\overrightarrow{OI}=\dfrac{1}{2}\left(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{x}+\overrightarrow{y}\right)\)
\(\overrightarrow{AC'}+\overrightarrow{CA'}+\overrightarrow{BD'}+\overrightarrow{DB'}\)
\(=2\left(\overrightarrow{OC'}+\overrightarrow{OA'}\right)+2\left(\overrightarrow{OD'}+\overrightarrow{OB'}\right)\)
\(=2.\left(-2\overrightarrow{OI}\right)+2.\left(-2\overrightarrow{OI}\right)\)
\(=-4.2\overrightarrow{OI}\)
\(\Rightarrow2\overrightarrow{OI}=-\dfrac{1}{4}\left(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{x}+\overrightarrow{y}\right)\)
Bài 1: Khoanh vào chữ cái đặt trước câu trả lời đúng: Câu 1: Công thức tính thể tích hình hộp chữ nhật là:
A. V = a x b + c B. V = a : b : c C. V = (a + b) x c D. V = a x b x c Câu 2:Thể tích của một hộp sữa có chiều dài 5,5 cm, chiều rộng 3,2 cm và chiều cao 10,4 cm là: A. 90,48 cm2 B. 90,48 cm3 C. 183,04 cm2 D. 183,04 cm3 bài 2 Tìm x: a) 53,2 : (x – 3,5) = 99 – 45,8 b) 4,2 x (x + 41,53) = 53,5 + 125 bài 3 Một bể bơi có chiều dài 12m, chiều rộng 5m và sâu 2,75m. Hỏi người thợ phải dùng bao nhiêu viên gạch men để lát đáy và xung quanh thành bể đó? Biết rằng mỗi viên gạch có chiều dài 25cm, chiều rộng 20 cm và diện tích mạch vữa lát không đáng kể.Cho hình hộp chữ nhật ABCD.A′B′C′D′ có đáy là hình vuông cạnh a và cạnh bên bằng 3a. Diện tích xung quanh Sxq của hình nón có đỉnh là tâm O của hình vuông A′B′C′D′ và có đáy là hình tròn nội tiếp hình vuông ABCD là
A. S xq = 13 πa 2 4
B. S xq = 37 πa 2 12
C. S xq = 13 πa 2 12
D. S xq = 37 πa 2 4
Để tìm chiều cao (c) của một hình hộp chữ nhật khi biết thể tích ( V ), chiều dài (a), chiều rộng (b). Ta làm như sau :
A. c = V x a : b B. c = V x ( a : b) C. c = V : a : b D. c = V : a x b