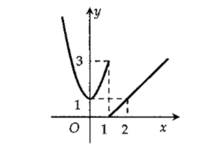
Hàm số y = f(x) có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu?
A. 0
B. 1
C. 2
D. 3
- Quan sát đồ thị ta thấy:
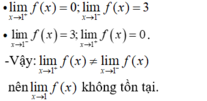
- Do đó hàm số gián đoạn tại điểm x = 1.
Chọn B.
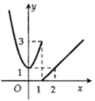
Hàm số y = f(x) có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu?
A. 0
B. 1
C. 3
D. 2
Đáp án B
- Phương pháp: Hàm số y = f(x) liên tục tại điểm x = x0 khi và chỉ khi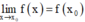 
- Cách giải:
+ Dễ thấy hàm số liên tục trên (-∞ ; 1) và (1 ; +∞)
+ Dựa vào đồ thị hàm số ta thấy
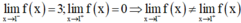
→ Do đó không tồn tại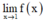 
, đồng nghĩa với việc hàm số gián đoạn tại x = 1.
Cho hàm số f ( x ) = x 2 - 4 Chọn câu đúng trong các câu sau: Cho hàm sô f(x) = căn bậc hai x^2 - 4
(I) f(x) liên tục tại x = 2.
(II) f(x) gián đoạn tại x = 2
(III) f(x) liên tục trên đoạn [-2; 2].
A. Chỉ (I) và (III).
B. Chỉ (I).
C. Chỉ (II).
D. Chỉ (II) và (III).
Chọn B.
Ta có: D = (-∞; -2] ∪ [2; +∞).
.và f(2) = 0.
Vậy hàm số liên tục tại x = 2.
Với -2 < x < 2 thì hàm số không xác định.
Cho đồ thị hàm số y = 1 2 ( x - 1 ) ( x 2 - 4 ) như hình vẽ bên. Số điểm cực trị của đồ thị hàm số f(x)=|(|x-1| ( x 2 - 4 ) +m)| , với m thuộc đoạn (2;6) là
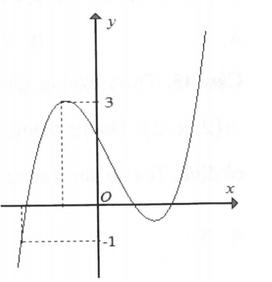
A. 6.
B. 3.
C. 7.
D. 5.
Cho đồ thị hàm số
y
=
1
2
(
x
-
1
)
(
x
2
-
4
)
như hình vẽ bên. Số điểm cực trị của đồ thị hàm số
f
(
x
)
=
x
-
1
(
x
2
-
4
)
+
m
, với m thuộc đoạn (2;6) là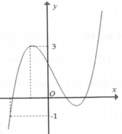
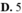
Cho hàm số f ( x ) = 1 + cos x k h i sin x ⩾ 0 3 - cos x k h i sin x < 0 . Hàm số có bao nhiêu điểm gián đoạn trên khoảng (0;2019)?
A.Vô số
B.320
C.321
D.319
Cho hàm số f x = x + 1 2 , x > 1 x 2 + 3 , x < 1 k 2 , x = 1 . Tìm k để f(x) gián đoạn tại x = 1.
A. k ≠ ± 2
B. k ≠ 2
C. k ≠ - 2
D. k ≠ ± 1
+ TXĐ: D = R
+ Với x = 1 ta có f ( 1 ) = k 2
+ Với x ≠ 1 ta có:
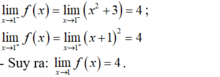
- Vậy để hàm số gián đoạn tại x = 1 khi:
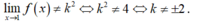
Chọn A.
Cho hàm số f x = x + 1 2 , x > 1 x 2 + 3 , x < 1 k 2 , x = 1 . Tìm k để f(x) gián đoạn tại x= 1.
A. k ≠ ± 2
B. k ≠ 2
C. k ≠ - 2
D. k ≠ ± 1
Với x= 1 ta có : f 1 = k 2
Với x ≠ 1 ta có :
lim x → 1 − f x = lim x → 1 − x 2 + 3 = 4 ; lim x → 1 + f x = lim x → 1 + x + 1 2 = 4 suy ra lim x → 1 f x = 4
Vậy để hàm số gián đoạn tại x= 1 khi lim x → 1 f x ≠ k 2 ⇔ k 2 ≠ 4 ⇔ k ≠ ± 2
Chọn đáp án A
Cho hàm số y = ax2a) Xác định a để đồ thị của hàm số trên đi qua điểm A (4 ; 4).
b) Vẽ đồ thị của hàm số trên với a vừa tìm được và đồ thị của hàm số y = \(-\dfrac{1}{2}x\) trên cùng một mặt phẳng tọa độ Oxy.
c) Tìm tọa độ giao điểm của hai hàm số trên (câu b) bằng phép toán.
a) Để đồ thị hàm số \(y=ax^2\) đi qua điểm A(4;4) thì
Thay x=4 và y=4 vào hàm số \(y=ax^2\), ta được:
\(a\cdot4^2=4\)
\(\Leftrightarrow a\cdot16=4\)
hay \(a=\dfrac{1}{4}\)
a, - Thay tọa độ điểm A vào hàm số ta được : \(4^2.a=4\)
\(\Rightarrow a=\dfrac{1}{4}\)
b, Thay a vào hàm số ta được : \(y=\dfrac{1}{4}x^2\)
- Ta có đồ thì của hai hàm số :
c, - Xét phương trình hoành độ giao điểm :\(\dfrac{1}{4}x^2=-\dfrac{1}{2}x\)
\(\Leftrightarrow x^2+2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy hai hàm số trên cắt nhau tại hai điểm : \(\left(0;0\right);\left(-2;1\right)\)
