Đáp án D

Đồ thị hàm số  y = 1 2 x - 3  có hai đường tiệm cận đứng và một đường tiệm cận ngang

Đồ thị hàm số  y = x + x 2 + x + 1 x   có 1 tiệm cận đứng là x = 0 

Mặt khác  lim x → + ∞ y = x + x 2 + x + 1 x = lim x → + ∞ x + x + 1 x + 1 x 2 x = 0  nên đồ thị hàm số có 2 tiệm cận ngang

Xét hàm số  y = x - 2 x - 1 x 2 - 1 = x - 2 x - 1 x + 2 x - 1 x 2 - 1 = x - 1 x + 2 x - 1 x - 1 x > 1 2  suy ra đồ thị không có tiệm cận đứng. Do đó có 1 mệnh đề đúng

Do

nên x = 1 là tiệm cận đứng.

Mặt khác,

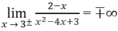
nên x = 3 cũng là tiệm cận đứng.

Vì

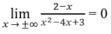
nên y = 0 là tiệm cận ngang.

Phương pháp:

Dựa vào các tính chất của đồ thị hàm số mũ và hàm số logarit.

Cách giải:

Cả 4 phát biểu đều đúng
Chọn C

TXĐ: R.

Từ

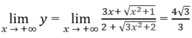
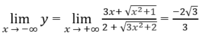
Ruy ra đồ thị hàm số có các tiệm cận ngang:

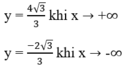
Đồ thị hàm số không có tiệm cận đứng.

Vì

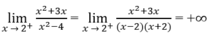
và

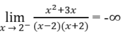
nên x = 2 là một tiệm cận đứng.

Do

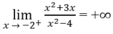
và

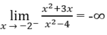
nên x = -2 là tiệm cận đứng thứ hai.

Ta lại có

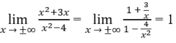
nên y = a là tiệm cận ngang.

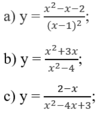
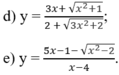
a) Vì

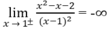
nên x = 1 là tiệm cận đứng.

Từ

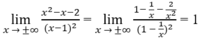
Suy ra y = 1 là tiệm cận ngang.

b) Vì

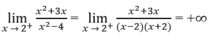
và

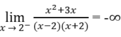
nên x = 2 là một tiệm cận đứng.

Do

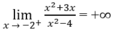
và

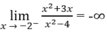
nên x = -2 là tiệm cận đứng thứ hai.

Ta lại có

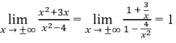
nên y = a là tiệm cận ngang.

c) Do

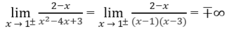
nên x = 1 là tiệm cận đứng.

Mặt khác,

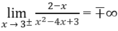
nên x = 3 cũng là tiệm cận đứng.

Vì

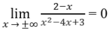
nên y = 0 là tiệm cận ngang.

d) TXĐ: R.

Từ

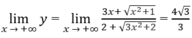
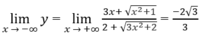
Ruy ra đồ thị hàm số có các tiệm cận ngang:

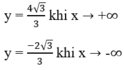
Đồ thị hàm số không có tiệm cận đứng.

e) TXĐ: D = (-∞; -√2) ∪ (√2;4) ∪ (4; +∞)

Do

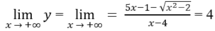
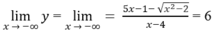
Cho nên đồ thị hàm số có hai tiệm cận ngang

y = 4 khi x ⇒ +∞

y = 6 khi x ⇒ -∞

Vì

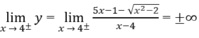
Cho nên đường thẳng x = 4 là tiệm cận đứng của đồ thị hàm số.

TXĐ: D = (- ∞ ; - 2 ) ∪ ( 2 ;4) ∪ (4; + ∞ )

Do

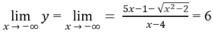
Cho nên đồ thị hàm số có hai tiệm cận ngang

y = 4 khi x ⇒ + ∞

y = 6 khi x ⇒ - ∞

Vì

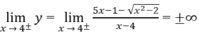
Cho nên đường thẳng x = 4 là tiệm cận đứng của đồ thị hàm số.

Chọn D

Đáp án D