Xác định m để mỗi cặp phương trình sau tương đương
![]()
Xác định m để mỗi cặp phương trình sau tương đương
![]()
![]()
Suy ra x = 1 và x = -4 là nghiệm của phương trình m x 2 - 4 x - m + 4 = 0
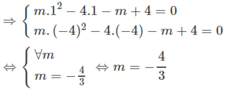
Xác định m để mỗi cặp phương trình sau tương đương
3x - 2 = 0 và (m + 3)x - m + 4 = 0
Phương trình 3x – 2 = 0 có nghiệm x = 2/3, thay x = 2/3 vào phương trình
(m + 3)x - m + 4 = 0 , ta có
2(m + 3) / 3 - m + 4 = 0
⇔ -m / 3 + 6 = 0 ⇔ m = 18
Với m = 18 phương trình (m + 3)x - m + 4 = 0 trở thành 21x = 14 hay x = 2/3
Vậy hai phương trình tương đương khi m = 18.
Xác định m để mỗi cặp phương trình sau tương đương
x + 2 = 0 và m ( x 2 + 3 x + 2 ) + m 2 x + 2 = 0
Phương trình x + 2 = 0 có nghiệm x = -2. Thay x = -2 vào phương trình
m ( x 2 + 3 x + 2 ) + m 2 x + 2 = 0 , ta có
-2m2 + 2 = 0 ⇔ m = 1 hoặc m = -1
Khi m = 1 phương trình thứ hai trở thành
x 2 + 4 x + 4 = 0
⇔ x = -2
Khi m = -1 phương trình thứ hai trở thành
- x 2 - 2 x = 0
⇔ -x(x + 2) = 0
Phương trình này có hai nghiệm x = 0 , x = -2.
Vậy hai phương trình đã cho tương đương khi m = 1.
Xác định tham số m để các cặp phương trình sau tương đương
![]()
Phương trình x 2 - 9 = 0 có hai nghiệm x =3 và x =-3
Giá trị x = 3 là nghiệm của phương trình
2 x 2 + (m - 5)x - 3(m + 1) = 0
Khi 18 + 3(m - 5) - 3(m + 1) = 0
Đẳng thức trên thỏa mãn với mọi m.
Giá trị x = -3 là nghiệm của hệ phương trình (1) khi
18 + 3(m - 5) - 3(m + 1) = 0
⇔ 30 - 6m = 0 ⇔ m = 5
Khi m = 5 phương trình (1) trở thành
2 x 2 - 18 = 0 ⇔ x 2 - 9 = 0
Phương trình này có hai nghiệm x = 3 và x = -3.
Vậy với m = 5 hai phương trình đã cho tương đương.
Xác định tham số m để các cặp phương trình sau tương đương
![]()
Phương trình x + 2 = 0 có nghiệm x = -2.
Phương trình ![]() có nghiệm duy nhất x = -2 khi -2m + 3m – 1 = 0 suy ra m = 1.
có nghiệm duy nhất x = -2 khi -2m + 3m – 1 = 0 suy ra m = 1.
Vậy hai phương trình tương đương khi m = 1.
Xác định m để 2 phương trình sau tương đương
2(x-5)=x-7và (m-4)x=m+6
Xác định m để mỗi cặp phương trình sau tương đương :
a) \(3x-1=0\) và \(\dfrac{3mx+1}{x-2}+2m-1=0\)
b) \(x^2+3x-4=0\) và \(mx^2-4x-m+4=0\)
- Điều kiện cần:
Phương trình \(3x-1\) có nghiệm là \(x=\dfrac{1}{3}\).
Điều kiện xác định của \(\dfrac{3mx+1}{x-2}+2m-1=0\) là \(x\ne2\).
Để cặp phương trình tương đương thì phương trình \(\dfrac{3mx+1}{x-2}+2m-1=0\) có nghiệm duy nhất là \(x=\dfrac{1}{3}\).
Từ đó suy ra: \(\dfrac{3m.\dfrac{1}{3}+1}{\dfrac{1}{3}-2}+2m-1=0\)\(\Leftrightarrow-\dfrac{3}{5}\left(m+1\right)+2m-1=0\)\(\Leftrightarrow\dfrac{7}{5}m-\dfrac{8}{5}=0\)\(\Leftrightarrow m=\dfrac{8}{7}\).
- Điều kiện đủ
Thay \(m=\dfrac{8}{7}\) vào phương trình \(\dfrac{3mx+1}{x-2}+2m-1=0\) ta được:
\(\dfrac{3.\dfrac{8}{7}x+1}{x-2}+2.\dfrac{8}{7}-1=0\)\(\Leftrightarrow\dfrac{24}{7}x+1+\dfrac{9}{7}\left(x-2\right)=0\)\(\dfrac{33}{7}x-\dfrac{11}{7}\)\(\Leftrightarrow x=\dfrac{1}{3}\).
Vậy \(m=\dfrac{8}{7}\) thì cặp phương trình tương đương.
\(x^2+3x-4=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-4\end{matrix}\right.\).
Để cặp phương trình tương đương thì \(mx^2-4x-m+4=0\) có hai nghiệm là \(x=1\) và \(x=-4\) .
Với \(x=1\) ta có: \(m.1^2-4.1-m+4=0\)\(\Leftrightarrow0=0\).
Vậy phương trình \(mx^2-4x-m+4=0\) luôn có một nghiệm \(x=1\).
Thay \(x=-4\) ta có: \(m.\left(-4\right)^2-4.\left(-4\right)-m+4=0\)\(\Leftrightarrow m=-\dfrac{4}{3}\).
Vậy \(m=-\dfrac{4}{3}\) thì cặp phương trình tương đương.
Em hãy chọn khẳng định đúng trong hai khẳng định sau đây:
a. Hai phương trình tương đương với nhau thì phải có cùng điều kiện xác định.
b.Hai phương trình có cùng điều kiện xác định có thể không tương đương với nhau.
Chọn câu có khẳng định đúng. Các cặp phương trình sau đây, cặp nào tương đương với nhau.
A. 3 ( 2 x + 5 ) = 0 v à 5 ( 5 x + 2 ) = 0
B. 5 ( 2 x - 3 ) = 0 v à x ( 2 x + 3 ) = 0
C. x 2 + 1 = 0 v à x 2 - 1 = 0
D. 3 ( 4 x + 3 ) = 0 v à 5 ( 4 x + 3 ) = 0