Cho F(x) = a x (lnx+b) là một nguyên hàm của hàm số f ( x ) = 1 + ln x x 2 trong đó a,b ∈ Z. Tính S = a+b
A. S = -2
B. S = 1
C. S = 2
D. S = 0
Cho F ( x ) = - 1 3 x 3 là một nguyên hàm của hàm số f ( x ) x Tìm nguyên hàm của hàm số f'(x)lnx
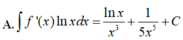
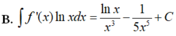
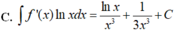
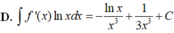
Cho F ( x ) = a x ( ln x + b ) là một nguyên hàm của hàm số f ( x ) = 1 + ln x x 2 , trong đó a , b ∈ ℤ . Tính S = a + b
A. S = -2
B. S = 1
C. S = 2
D. S = 0
Cho F(x) = 1 2 x 2 là 1 nguyên hàm của hàm số f ( x ) x . Tìm nguyên hàm của hàm số f'(x)lnx
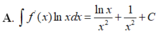
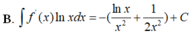
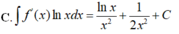
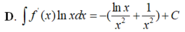
Cho F x = - 1 3 x 3 là một nguyên hàm của hàm số f x x . Tìm nguyên hàm của hàm số f'(x)lnx.
A. ∫ f ' x d x = ln x x 3 + 1 3 x 3 + C
B. ∫ f ' x d x = - ln x x 3 + 1 3 x 3 + C
C. ∫ f ' x d x = - ln x x 3 + 1 5 x 3 + C
D. ∫ f ' x d x = ln x x 3 + 1 5 x 3 + C
Cho F x = − 1 3 x 3 là một nguyên hàm của hàm số f x x . Tìm nguyên hàm của hàm số f '(x).lnx
A. ∫ f ' x lnxdx = lnx x 3 + 1 5 x 5 + C .
B. ∫ f ' x lnxdx = lnx x 3 − 1 5 x 5 + C .
C. ∫ f ' x lnxdx = lnx x 3 + 1 3 x 3 + C .
D. ∫ f ' x lnxdx = − lnx x 3 + 1 3 x 3 + C .
Đáp án C
F x = − 1 3 x 3 là một nguyên hàm của f x x nên
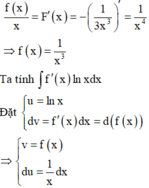
Áp dụng công thức nguyên hàm từng phần ta có
∫ f ' x lnxdx = ∫ lnxd f x = lnx . f x − ∫ f x x dx = lnx x 3 + 1 3 x 3 + C
Họ nguyên hàm F(x) của hàm số f ( x ) = x lnx là
A. F ( x ) = x 2 2 lnx - x 2 2 + C
B. F ( x ) = x 2 2 lnx - x 2 4 + C
C. F ( x ) = x 2 2 lnx + x 2 2 + C
D. F ( x ) = x 2 2 lnx + x 2 4 + C
Một nguyên hàm F(x) của hàm số f ( x ) = ln x + x 2 + 1 thỏa mãn F(0) = 1. Chọn kết quả đúng
![]()
![]()
![]()
![]()
Chọn A.
Đặt u = ln x + x 2 + 1 , d v = d x ta được
F(x)=x ln x + x 2 + 1 - x 2 + 1 + C
Vì F(0) = 1 nên C = 2
Vậy ![]()
Cho f(x) =\(\frac{1}{2x^2}\)là một nguyên hàm của hàm số \(\frac{f\left(x\right)}{x}\). Tìm nguyên hàm của hàm số \(f'\left(x\right)lnx\)
Xin mn giải giúp em ạ
Họ nguyên hàm của hàm số f(x)=4x(1+lnx) là
![]()
![]()
![]()
![]()