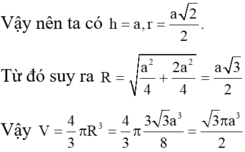Tính tỉ số thể tích giữa khối lập phương và khối cầu ngoại tiếp khối lập phương đó.
A. π 3 2
B. 2 π 3
C. π 2 3
D. 3 π 2
Một khối cầu ngoại tiếp khối lập phương. Tỷ số thể tích giữa khối cầu và khối lập phương là
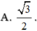
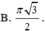
![]()
Một hình lập phương cạnh bằng a nội tiếp khối cầu ( S 1 ) và ngoại tiếp khối cầu ( S 2 ) , gọi V 1 và V 2 lần lượt là thể tích của các khối S 1 và ( S 2 ) . Tính tỉ số k = V 1 V 2
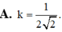
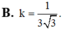
![]()
![]()
Cho khối cầu (S) tâm O, bán kính R ngoại tiếp khối lập phương (P) và nội tiếp khối trụ (T). Gọi V 1 , V 2 lần lượt là thể tích của khối lập phương (P) và khối trụ (T). Tính giá trị gần đúng của tỉ số V 1 V 2
A. 0,23
B. 0,24
C. 0,25
D. 0,26
Để ý rằng đường chéo của hình lập phương chính là đường kính của khối cầu. Mặt khác ta lại có công thức: “Bình phương độ dài đường chéo của hình lập phương bằng ba lần bình phương của độ dài cạnh hình lập phương”. Khi đó 2 R 2 = 3 a 2 ⇒ a = 2 R 3 3
Suy ra V 1 = 2 3 3 R 3 = 8 3 9 R 3 .
Vì khối cầu có bán kính R nên ta có thể tính được bán kính và chiều cao của khối trụ ngoại tiếp ngoài khối cầu lần lượt là R và 2R.
Do đó V 2 = πR 2 . 2 = 2 πR 3
Vậy ta có tỉ số V 1 V 2 = 8 3 9 R 3 2 πR 3 = 4 3 9 π ≈ 0 , 245
Đáp án C
Một hình lập phương cạnh bằng a nội tiếp khối cầu S 1 và ngoại tiếp khối cầu S 2 , gọi V 1 và V 2 lần lượt là thể tích của các khối S 1 và S 2 . Tính tỉ số k = V 1 V 2 .
A. k = 1 2 2
B. k = 1 3 3
C. k = 2 2
D. 3 3
Đáp án D
Gọi khối lập phương cần xét ABCD.A'B'C'D' cạnh a.
Bán kính mặt cầu ngoại tiếp khối cầu là R 2 = A A ' 2 = a 2 ⇒ V 1 = 4 3 R 2 3 .
Bán kính mặt cầu ngoại tiếp khối cầu là
R 1 = A C ' 2 = A B 2 + A D 2 + A A ' 2 2 = a 3 2 ⇒ V 1 = 4 3 πR 3 1
Vậy tỉ số k = V 1 V 2 = R 3 1 R 3 1 = R 1 R 2 3 = 3 3 = 3 3 .
Một khối lập phương có thể tích 2 2 . Khi đó thể tích khối cầu ngoại tiếp hình lập phương đó bằng:
A. 2 π
B. 6 π
C. 2π
D. 6π
Chọn B.
Với ![]() là cạnh của hình lập phương. Ta có CT
là cạnh của hình lập phương. Ta có CT
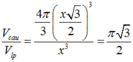
Áp dụng CT suy ra Vcầu = π 6
Một hình lập phương có cạnh bằng 2a vừa nội tiếp hình trụ (T) vừa nội tiếp mặt cầu (C) và hai đáy của hình lập phương nằm trên 2 đáy của hình trụ. Tính tỉ số thể tích V c V T giữa khối cầu và khối trụ giới hạn bởi (C) và (T) ?
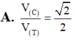
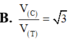
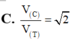
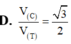
Một hình lập phương có cạnh bằng 2a vừa nội tiếp hình trụ (T) vừa nội tiếp mặt cầu (C) và hai đáy của hình lập phương nằm trên 2 đáy của hình trụ. Tính tỉ số thể tích V C V T giữa khối cầu và khối trụ giới hạn bởi (C) và (T) ?
A. V C V T = 2 2
B. V C V T = 3
C. V C V T = 2
D. V C V T = 3 2
Đáp án là B.
+ Ta có: R C = a 3 ⇒ V C = 4 3 π .3 3 a 3 = 4 π a 3 3 .
+ R T = a 2 ⇒ V T = 2 a .. π 2 a 2 = 4 π a 3
Vậy V C V T = 3 .
Cho một hình cầu và một hình lập phương ngoại tiếp nó. Tính tỉ số phần trăm giữa:
a, Diện tích mặt cầu và diện tích xung quanh của hình lập phương;
b, Thể tích hình cầu và thể tích của hình lập phương.
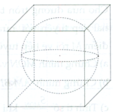
a, Tính được S S x q = 78,5%
b, Tính được V h c V h l p = 52 , 4 %
Tính thể tích khối cầu ngoại tiếp hình lập phương có cạnh bằng a
A. V = πa 3 3 2
B. V = 4 πa 3 3
C. V = πa 3 3 8
D. V = 4 πa 3 3 3
A
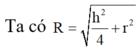
Trong đó R là bán kính khối cầu, h là chiều cao hình lập phương, r là bán kính đuờng tròn ngoại tiếp đáy.