Chọn B.
Với ![]() là cạnh của hình lập phương. Ta có CT
là cạnh của hình lập phương. Ta có CT
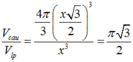
Áp dụng CT suy ra Vcầu = π 6
Chọn B.
Với ![]() là cạnh của hình lập phương. Ta có CT
là cạnh của hình lập phương. Ta có CT
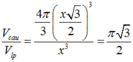
Áp dụng CT suy ra Vcầu = π 6
Một hình lập phương có diện tích mặt chéo bằng a 2 2 . Gọi V là thể tích khối cầu và S là diện tích mặt cầu ngoại tiếp hình lập phương nói trên. Khi đó tích S.V bằng
A. S V = 3 π 2 a 5 2
B. S V = 3 3 π 2 a 5 2
C. S V = 3 6 π 2 a 5 2
D. S V = 3 π 2 a 5 2
Tính tỉ số thể tích giữa khối lập phương và khối cầu ngoại tiếp khối lập phương đó.
A. π 3 2
B. 2 π 3
C. π 2 3
D. 3 π 2
Tính thể tích khối cầu ngoại tiếp hình lập phương có cạnh bằng a
A. V = πa 3 3 2
B. V = 4 πa 3 3
C. V = πa 3 3 8
D. V = 4 πa 3 3 3
Cho hình lập phương có cạnh bằng a. Tính theo a thể tích của khối cầu tiếp xúc với 12 cạnh của hình lập phương đó.
A. π a 3 6
B. 4 π a 3 3
C. π 2 a 3 3
D. π 3 a 3 2
Tính thể tích của khối cầu ngoại tiếp hình lập phương cạnh a bằng
A. πa 3
B. 4 πa 3 3
C. πa 3 3 3
D. πa 3 3 2
Một hình lập phương có cạnh bằng 2a vừa nội tiếp hình trụ (T) vừa nội tiếp mặt cầu (C) và hai đáy của hình lập phương nằm trên 2 đáy của hình trụ. Tính tỉ số thể tích V C V T giữa khối cầu và khối trụ giới hạn bởi (C) và (T) ?
A. V C V T = 2 2
B. V C V T = 3
C. V C V T = 2
D. V C V T = 3 2
Một khối trụ có hai đáy là hai hình tròn ngoại tiếp hai mặt của một hình lập phương cạnh a. Tính theo a thể tích V của khối trụ đó
A. V = π a 3 2
B. V = π a 3 4
C. V = π a 3
D. V = 2 π a 3
Một hình lập phương cạnh bằng a nội tiếp khối cầu S 1 và ngoại tiếp khối cầu S 2 , gọi V 1 và V 2 lần lượt là thể tích của các khối S 1 và S 2 . Tính tỉ số k = V 1 V 2 .
A. k = 1 2 2
B. k = 1 3 3
C. k = 2 2
D. 3 3
Tính thể tích V của khối cầu ngoại tiếp hình lập phương cạnh a
A. V = πa 3
B. V = 4 πa 3 3
C. V = 2 πa 3 3
D. V = 3 πa 3 2