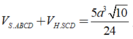Hình bên cho biết A O M ^ = 45 ∘ , M O B ^ = 15 ∘ và A O B ^ = 60 ∘ . Trong ba tia O A , O B , O M tia nào nằm giữa hai tia còn lại?
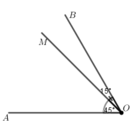
Trên hình vẽ bên biết MN // PQ // OE và M ^ = 45 ° , P ^ = 130 ° . Tính M O P ^
Vì MN // OE nên O M N ^ = M O E ^ = 45 ° (hai góc so le trong)
PQ // OE nên O P Q ^ + P O E ^ = 180 ° ( hai góc trong cùng phía)
Mà O P Q ^ = 130 ° do đó P O E ^ = 180 ° − 130 ° = 50 °
Vậy M O P ^ = M O E ^ + E O P ^ = 45 ° + 50 ° = 95 °
Cho hình chữ nhật ABCD, M là điểm tùy ý sao cho \(\widehat{AMC}=45^o;\widehat{BMD}=60^o\) . Biết SAMD = 265. Tính SBMD.
Cho hình vuông ABCD có cạnh bằng a. Một góc 45 độ quay xung quanh đỉnh A và nằm bên trong hình vuông cắt cạnh BC,CD lần lượt tại M và N.
1) C/m MN luôn tiếp xúc với một đường tròn cố định.
2) C/m a2- BM.DN=a(BM+DN)
Cho hình vẽ bên : Biết a//b , A¹= 150° ,B²= 45° Tính số đo của góc AOB
Cho hình thang cân ABCD ( AB//CD) và góc C = góc D=45 độ . M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA biết cạnh bên bằng 6cm. Tính diện tích MNPQ.
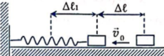
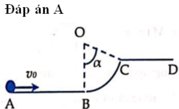
Vật nhỏ m được truyền vận tốc ban đầu theo phương ngang v0 = 8m/s từ A sau đó m đi lên theo đoạn đường tròn BC tâm O, bán kính OC = 2m phương OB thẳng đứng, góc α = 45 ° và m rơi xuống tại D (hình bên). Bỏ qua ma sát và sức cản của không khí. Lấy g = 10m/s2. Khoảng cách CD bằng
A. 5,2 m
B. 10,4 m
C. 9,2m
D. 11,3 m
- Áp dụng định luật bảo toàn cơ năng với gốc thế năng trọng trường là B:
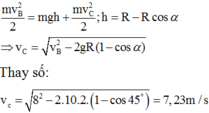
- Khi rời C chuyển động của vật là chuyển động ném xiên với

- Khoảng cách CD chính là tầm bay xa của vật ném xiên:
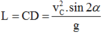
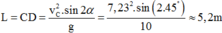
cho hình lăng trụ ABCDA'B'C'D' đáy là hình chữ nhật tâm O. AB=a, AD=a✓3. a'o vuông góc với đáy. cạnh bên AA' tạo với đáy 1 góc 45°. tính VABCDA'B'C'D'
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, SO vuông góc với mặt phẳng đáy, mặt bên (SAB) là tam giác đều cạnh a và hợp với đáy 1 góc 450. Gọi M, N lần lượt là trung điểm của AB và AD. Tính thể tích khối chóp S.ABCD và khoảng cách giữa SM và NC
❤sin45=\(\dfrac{SO}{SM}\) => SO=sin45 . SM= \(\dfrac{\sqrt{2}}{2}.\dfrac{a\sqrt{3}}{2}\) = \(\dfrac{a\sqrt{6}}{4}\)
OM= \(\sqrt{SM^2-SO^2}\) = \(\dfrac{a\sqrt{6}}{4}\)
BC = 2OM => BC=\(\dfrac{a\sqrt{6}}{2}\)
V = \(\dfrac{1}{3}.AB.BC.SO=\dfrac{1}{3}.a.\dfrac{a\sqrt{6}}{2}.\dfrac{a\sqrt{6}}{4}=\dfrac{a^3}{4}\)
❤ta có: SM⊂ (SAB) (1)
mà: \(\left\{{}\begin{matrix}NC//AB\\AB\subset\left(SAB\right)\end{matrix}\right.\) => NC// (SAB) (2)
từ (1) và (2) => SM//NC
\(d_{\left(SM,NC\right)}=d_{\left(NC,\left(SAB\right)\right)}=d_{\left(N,\left(SAB\right)\right)}=2d_{\left(O,\left(SAB\right)\right)}\)
+kẻ OH⊥SM
+ Ta có: \(\left\{{}\begin{matrix}AB\perp OM\\AB\perp SO\end{matrix}\right.\) => AB ⊥ (SOM) \(\supset OH\)
=> \(\left\{{}\begin{matrix}OH\perp AB\\OH\perp SM\end{matrix}\right.\) => OH⊥(SAB)
➜d(O,(SAB)) =OH
OH=\(\dfrac{OM.SO}{\sqrt{OM^2+SO^2}}\)\(\dfrac{a\sqrt{3}}{4}\)
➜d(N,(SAB)) =d(SM,NC)= \(\dfrac{a\sqrt{3}}{2}\)
Cho hình vẽ bên với AB là đường kính DA và DC là 2 tiếp tuyến với đường tròn (O). Biết góc ABC có số đo là 45 độ .Số đo góc ADC bằng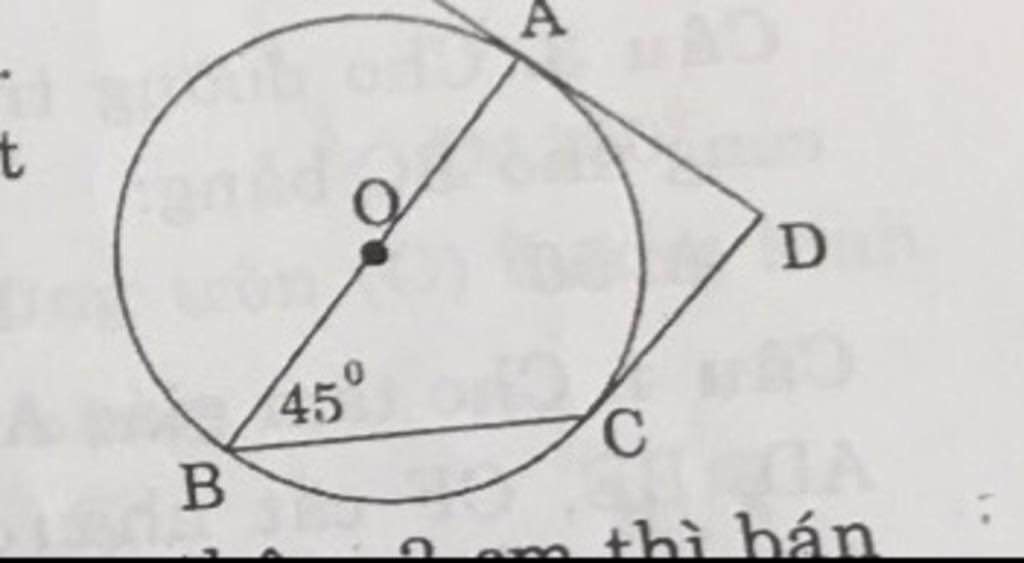
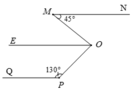
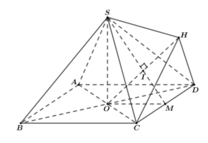
Cho khối chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh bằng a, tâm O cạnh bên bằng a 3 . Gọi M là trung điểm của CD, H là điểm đối xứng của O qua SM (tham khảo hình vẽ bên). Thể tích khối đa diện ABCDSH bằng
A. a 3 10 12
B. a 3 10 18
C. a 3 10 24
D. 5 a 3 10 24
Chọn D
Khối đa diện ABCDSH được chia thành hai khối chóp S.ABCD và H.SCD

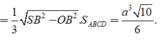
Vì H là điểm đối xứng của O qua SM nên
![]()

Vậy thể tích khối đa diện cần tính bằng