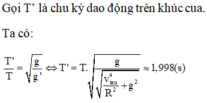
Một tàu lượn bằng đồ chơi chuyển động không ma sát trên đường ray như hình vẽ. Khối lượng tàu 50g, bán kính đường tròn R = 20cm. Độ cao h tối thiểu khi thả tàu để nó đi hết đường tròn là?
A. 80cm
B. 50cm
C. 40cm
D. 20cm
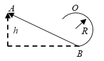
Một tàu lượn bằng đồ chơi chuyển động không ma sát trên đường ray như hình vẽ. Khối lượng tàu 50g, bán kính đường tròn R=20cm. Độ cao h tối thiểu khi thả tàu để nó đi hết đường tròn là?
A. 80cm
B. 50cm
C. 40cm
D. 20cm
Đáp án B.
Vận tốc tại điểm cao nhất D.
![]()
Tại điểm D theo định luật 2 Niutơn ta có:
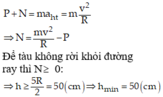
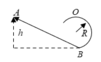
Một tàu lượn bằng đồ chơi chuyển động không ma sát trên đường ray như hình vẽ. Khối lượng tàu 50g, bán kính đường tròn R = 20cm. Độ cao h tối thiêu khi thả tàu đế nó đi hết đường tròn là?
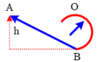
A. 80cm
B. 50cm
C. 40cm
D. 20cm
Một “vòng xiếc’’ có phần dưới được uốn thành vòng tròn có bán kính R như hình vẽ. Một vât nhỏ khối lượng m được buông ra trượt không ma sát dọc theo vòng xiếc.
a. Tìm độ cao tối thiểu h để vật có thể trượt hết vòng tròn. ứng dụng với bán kính vòng tròn là 20 cm
b. Nếu h = 60cm thì vận tốc của vật là bao nhiêu khi lên tói đỉnh vòng tròn

Chon mốc thế năng tại mặt đất. Theo định luật bảo toàn cơ năng
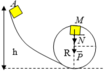
W A = W M ⇒ m g h = 1 2 m v M 2 + m g z M ⇒ 1 2 m . v M 2 = m g ( h A − 2 R ) ( 1 )
Mặt ta có :
P + N = m v M 2 R ⇒ N = m v M 2 R − m g
Để vật vẫn chuyển động trên vòng thì N ≥ 0
⇒ m v M 2 R − m g ≥ 0 ⇒ 1 2 m v M 2 ≥ m g R 2 ( 2 )
Từ ( 1 ) và ( 2 ) ta có
m g ( h − 2 R ) ≥ m g R 2 ⇒ h ≥ 2 R + R 2 = 5 R 2
Nếu R = 20cm thì chiều cao là
⇒ h ≥ 5.0 , 2 2 = 0 , 5 m = 50 c m
b. Từ ( 1 ) ta có
⇒ 1 2 m . v M 2 = m g ( h A − 2 R ) ⇒ v M = 2 g ( h − 2 R ) ⇒ v M = 2.10 ( 0 , 6 − 2.0 , 2 ) = 2 ( m / s )
đoàn tàu chạy trên một đường ray là 1 cung tròn có bán kính 560 m. đường sắt rộng 1,4 m và đường ray ngoài cao hơn đường ray trong 10 cm. hỏi tàu phải chạy với vận tốc bao nhiêu để gờ bánh không nén lên thành ray? cho \(\sin\alpha=\tan\alpha\) nếu góc α nhỏ.
Gọi lực nén là Q(N)
\(\Rightarrow Q\cos\alpha=P\)
Để gờ bánh ko nén lên thành \(\Rightarrow F_{ht}=Q.\sin\alpha=m.a_{ht}=\dfrac{m.v^2}{R}\)
\(\Rightarrow P\tan\alpha=\dfrac{mv^2}{R}\Rightarrow g\tan\alpha=\dfrac{v^2}{R}\)
\(\tan\alpha\approx\sin\alpha=\dfrac{10}{140}\Rightarrow v=\sqrt{R.g\tan\alpha}=20\left(m/s\right)\)
Một đoàn tàu khối lượng 100 tấn bắt đầu chuyển động với lực kéo 7.10⁴N và hệ số ma sát với đường ray bằng 0,05.Tính vận tốc và thời gian để tàu đi được 1km.Lấy g=10m/s²
Định luật ll Niu-tơn:
\(F_k-F_{ms}=m\cdot a\)
\(\Rightarrow F_k-\mu mg=m\cdot a\)
\(\Rightarrow7\cdot10^4-0,05\cdot100\cdot1000\cdot10=100\cdot1000\cdot a\)
\(\Rightarrow a=0,2\)m/s2
Thời gian tàu sau khi đi đc 1km=1000m:
\(S=\dfrac{1}{2}at^2\Rightarrow t=\sqrt{\dfrac{2S}{a}}=\sqrt{\dfrac{2\cdot1000}{0,2}}=100s\)
Vận tốc tàu sau khi đi đc 1km:
\(v=a\cdot t=0,2\cdot100=20\)m/s
Một đoàn tàu đang chuyển động với vận tốc thẳng đều với vận tốc v0 = 72km/h thì một số toa cuối (chiếm 25% tổng khối lượng đoàn tàu) bị tách ra khỏi đoàn tàu. Hỏi khi các toa đó dừng lại thì vận tốc của các toa ở phần đầu tàu là bao nhiêu? Biết lực kéo của đầu tàu không đổi; hệ số ma sát lăn giữa đường ray với mọi phần của đoàn tàu là như nhau, không đổi.
A. 96km/h.
B. 108km/h.
C. 150km/h.
D. 100km/h.
Đáp án A.
Gọi khối lượng cả đoàn tàu là m. Ban đầu chuyển động đều nên: F k = μ m g (1)
Khi đứt ra:
+ Định luật II Niu-tơn cho phần đầu tàu:

Một đầu tàu khi khởi hành cần một lực kéo 10000N, nhưng khi chuyển động thẳng đều trên đường sắt thì chỉ cần một lực kéo 5000N. Tìm độ lớn của lực ma sát khi bánh xe lăn đều trên đường sắt. Biết đầu tàu có khối lượng 10 tấn. Hỏi lực ma sát này có độ lớn bằng bao nhiêu phần trọng lượng của đoàn tàu?
Tàu có khối lượng 10 tấn nên trọng lượng của tàu là:
P = 10.m = 10.10000 = 100000 N
Khi bánh tàu lăn đều trên đường sắt thì lực kéo cân bằng lực cản nên lực ma sát bằng Fms = 5000N.
So với trọng lượng đầu tàu thì lực ma sát bằng:
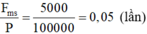
Một con lắc đơn được treo vào trần một toa của một đoàn tầu hỏa. Khi tàu đứng yên, con lắc dao động bé với chu kì 2 s. Một khúc cua mà đường ray nằm trên mặt phẳng nằm ngang có dạng một cung tròn bán kính cong 400 m. Cho biết gia tốc rơi tự do là g = 10 m/s2, bán kính cong là rất lớn so với chiều dài con lắc và khoảng cách giữa hai đường ray. Khi đoàn tàu này chuyển động với tốc độ không đổi 15 m/s trên khúc cua nói trên thì chu kì dao động nhỏ của con lắc gần với giá trị nào sau đây nhất?
A. 1,998 s.
B. 1,999 s.
C. 1,997 s.
D. 2,000 s.
Đáp án A
Khi vật chưa chuyển động chịu gia tốc trọng trường là g tìm được l .
Khi vật chuyển động với tốc độ v = 15 m/s chịu tác động của gia tốc trọng trường và gia tốc hướng tâm :
g' = g 2 + a h t 2
Chu kì dao động nhỏ của con lắc : T' = 2 π 1 g 2 + a ht 2
Một con lắc đơn được treo vào trần một toa của một đoàn tầu hỏa. Khi tàu đứng yên, con lắc dao động bé với chu kì 2 s. Một khúc cua mà đường ray nằm trên mặt phẳng nằm ngang có dạng một cung tròn bán kính cong 400 m. Cho biết gia tốc rơi tự do là g = 10 m / s 2 , bán kính cong là rất lớn so với chiều dài con lắc và khoảng cách giữa hai đường ray. Khi đoàn tàu này chuyển động với tốc độ không đổi 15 m/s trên khúc cua nói trên thì chu kì dao động nhỏ của con lắc gần với giá trị nào sau đây nhất?
A. 1,998 s.
B. 1,999 s.
C. 1,997 s.
D. 2,000 s.
Đáp án A
Tàu đi qua khúc cua => tàu chuyển động tròn đều => tàu có lực hướng tâm => con lắc chịu thêm lực quán tính (bằng với lực hướng tâm, cùng phương nhưng ngược chiều).