Chọn D.

Gọi cấp số nhân đó là (u_n), n = 1,7 ¯ . Theo đề bài ta có :

u 4 = 6 u 7 = 243 u 2 ⇔ u 1 . q 3 = 6 u 1 . q 6 = 243 u 1 . q ⇔ u 1 = 2 9 q = 3

Do đó các số hạng còn lại của cấp số nhân là

u 1 = 2 9 ; u 2 = 2 3 ; u 3 = 2 ; u 5 = 18 ; u 6 = 54 ; u 7 = 162

Đáp án C

Kí hiệu u1,u2,u3,u4,u5 là các số hạng của cấp số nhân

Ta có :

Đáp án C

Lời giải:

Gọi số đầu tiên trong csn trên là $u_1$ và công bội là $q$

$u_1-u_2=35$

$\Leftrightarrow u_1-u_1q=35$

$\Leftrightarrow u_1(1-q)=35(1)$

$u_3-u_4=560$

$\Leftrightarrow u_1q^2-u_1q^3=560$

$\Leftrightarrow u_1q^2(1-q)=560(2)$

Từ $(1); (2)\Rightarrow q^2=560:35=16$

$\Rightarrow q=\pm 4$

Nếu $q=4$ thì $u_1=\frac{-35}{3}$

$u_2=\frac{-35}{3}.4=\frac{-140}{3}; u_3=\frac{-140}{3}.4=\frac{-560}{3}; u_4=\frac{-2240}{3}$

Tương tự với $q=-4$

+ Gọi số hạng đầu của cấp số nhân là u1, công bội là x

Theo giả thiết ta có hệ phương trình

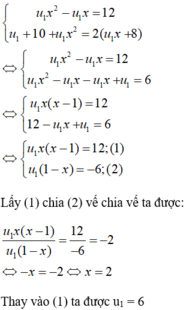
+ Tổng của năm số hạng đầu của CSN là:

ĐS: Cấp số cộng: 5, 25, 45

Cấp số nhân: 5, 15, 45

Gọi 3 số hạng của cấp số cộng là: \(5;5+d;5+2d\)
Gọi 3 số hạng của cấp số nhân là: \(5;5q;5q^2\).
Ta có hệ sau:\(\left\{{}\begin{matrix}5+2d=5q^2\\5+d=5q+10\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}5+2d=5q^2\\d=5q+5\end{matrix}\right.\)\(\Rightarrow5+2.\left(5q+5\right)=5q^2\)\(\Rightarrow\left\{{}\begin{matrix}q=-1\\q=3\end{matrix}\right.\).
Với \(q=-1\) thì \(d=5.q+5=5.\left(-1\right)+5=0\).
Với \(q=3\) thì \(d=5.q+5=5.3+5=20\).
Vậy
Với \(q=-1\):
3 số hạng của cấp số cộng là: 5; 5; 5.
3 số hạng của cấp số nhân là: 5; - 5; 5.
Với \(q=3\):
3 số hạng của cấp số cộng là: 5; 25; 45.
3 số hạng của cấp số nhân là: 5; 15; 45.

Chọn A

Gọi u1,u2,u3,u4 là 4 số hạng đầu tiên của cấp số nhân, với công bội q. gọi (vn) là cấp số cộng tương ứng với công sai là d. Theo giả thuyết Ta có:

u 1 + u 2 + u 3 = 16 4 9 u 1 = v 1 u 2 = v 4 = v 1 + 3 d u 3 = v 8 = v 1 + 7 d ⇔ u 1 + u 1 q + u 2 q 2 = 16 4 9    1 u 1 q = u 1 + 3 d                        2 u 1 q 2 = u 1 + 7 d                     3

Khử d từ (2) và (3) ta thu được: 

7 u 1 q = 7 u 1 + 21 d 3 u 1 q 2 = 3 u 1 + 21 d

Lấy vế trừ vế ta thu được 

7 u 1 q − 3 u 1 q 2 = 4 u 1 ⇔ u 1 . 3 q 2 − 7 q + 4 = 0 ⇔ u 1 = 0 3 q 2 − 7 q + 4 = 0

Do  u 1 ≠ 0 ⇒ q = 1 q = 4 3

Theo định nghĩa cấp số nhận thì q ≠ 1 . Do đó  q = 4 3

Thay q = 4 3 vào (1) ta được  u 1 = 4

Chọn đáp án D

u 4 = u 1 . q 3 = 48