Tổng các nghiệm của phương trình z + i 1 + i 3 - z 2 - 1 + 2 i z 2 i + 2 = 0 là:
A. 1 + 2i
B. 2 - i
C. 1 - 2i
D. 2 + i
Tổng các nghiệm của phương trình z . z 2 + z 2 + z - + 1 = 0 là:
A. 1
B. 1 + 2i
C. 0
D. -1
Cho phương trình: ( z2 - z) ( z + 3) (z + 2) = 10 .Tính tổng tất cả các phần thực của các nghiệm phương trình trên.
A. -1
B. -2
C. -3
D. -4
Chọn D.
Phương trình đã cho tương đương với phương trình
z( z + 2) ( z - 1) ( z + 3)
Hay ( z2 + 2z) ( z2 + 2z - 3) = 10
Đặt t = z2 + 2z. Khi đó phương trình trở thành: t2 - 2t – 10 = 0.
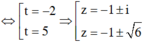
Vậy phương trình có các nghiệm: ![]()
Tổng tất cả các phần thực của các nghiệm phương trình đã cho là:
-1+ ( -1) + (-1) + ( -1) = -4.
z = 1 + i không là nghiệm của phương trình nào trong các phương trình sau?
![]()
![]()
![]()
![]()
z = 1 + i không là nghiệm của phương trình nào trong các phương trình sau?
A. x 2 - 2 x + 1 = 0
B. - 2 x 2 + 5 x - 5 - i = 0
C. 5 x 2 - x - 2 = 0
D. 3 x - 3 - 3 i = 0
Tổng phần thực các nghiệm phức của phương trình: z 2 - z - 1 + 3 i = 0 bằng
A. -1
B. 3
C. 1
D. -3
Gọi tổng cần tìm là T. Tính tổng bình phương các nghiệm của phương trình: z + 1 i z + 1 i 2 . . . . z + 1 i 15 = 0
A. T = 0
B. T = 4
C. T = 15i
D. T = 15 2
Gọi S là tổng các nghiệm phức của phương trình ( z - 1 ) 4 = 5. Tính S.
A. S = 0
B. S = 4
C. S = 2i
D. S = 4 5
Cho phương trình z 3 + a z 2 + b z + c = 0 nhận z = 2 và z = 1 + i làm các nghiệm của phương trình. Khi đó a - b + c là
![]()
![]()
![]()
![]()
Số phức z=a+bi, a,b thuộc R là nghiệm của phương trình ( z - 1 ) ( 1 + i z z - 1 z = i . Tổng T=a^2+b^2 bằng
A. ![]() .
.
B. ![]() .
.
C.![]()
D. ![]() .
.