Cho x, y là các số thực dương thay đổi. Xét hình chóp S.ABC có S A = x , B C = y , các cạnh còn lại đều bằng 1. Khi thể tích khối chóp S,ABC đạt giá trị lớn nhất thì tích x.y bằng
A. 4 3
B. 4 3 3
C. 2 3
D. 1 3
Cho x,y là các số thực dương thay đổi. Xét hình chóp S.ABC có SA= x,BC= y, các cạnh còn lại đều bằng 1. Khi thể tích khối chóp S.ABC đạt giá trị lớn nhất thì tích x+y bằng:
A. 4 3
B. 4 3 3
C. 2 3
D. 1 3
Cho hình chóp S.ABC có SA=SB=SC=AB=AC=a, BC=2x (trong đó a là hằng số và x thay đổi thuộc khoảng 0 ; a 3 2 . Tính thể tích lớn nhất Vmax của hình chóp S.ABC
![]()
![]()
![]()
![]()
có nge9ejr 0 uiwu3433r2///3
Cho hình chóp S.ABC có SA=SB=SC=AB=AC=a, BC=2x (trong đó a là hằng số và x thay đổi thuộc khoảng 0 ; a 3 2 ). Tính thể tích lớn nhất V m a x của hình chóp S.ABC
A. V m a x = a 3 6
B. V m a x = a 3 2 4
C. V m a x = a 3 8
D. V m a x = a 3 2 12
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = 1, AC = 2; cạnh bên SA vuông góc với đáy và SA = 1. Gọi I là trung điểm của AC. Xét M là điểm thay đổi trên cạnh AB sao cho A M = x ( 0 < x < 1 ) và (P) là mặt phẳng đi qua M, song song với SA và IB. Thiết diện của hình chóp với mặt phẳng (P) có diện tích lớn nhất thì giá trị của x bằng.
![]()
![]()
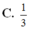
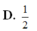
Xét x,y là hai số thực dương thay đổi thoả mãn điều kiện xy = 1. Tìm max của biểu thức A = \(\dfrac{2.\left(x^3+y^3\right)}{\left(x^4+y^2\right).\left(x^2+y^4\right)}\)
\(A=\dfrac{2\left(x^3+y^3\right)}{\left(x^4+y^2\right)\left(x^2+y^4\right)}=2.\dfrac{\left(x^3+y^3\right)}{x^4y^4+x^2y^2+x^6+y^6}\)
\(=2.\dfrac{\left(x^3+y^3\right)}{1+1+x^6+y^6}=2.\dfrac{x^3+y^3}{x^6+y^6+2x^3y^3}=2.\dfrac{x^3+y^3}{\left(x^3+y^3\right)^2}=\dfrac{2}{x^3+y^3}\left(1\right)\)
Áp dụng bất đẳng thức Cauchy ta có:
\(x^3+y^3+1\ge3\sqrt{xy.1}=3\)
\(\Rightarrow x^3+y^3\ge2\Rightarrow\dfrac{2}{x^3+y^3}\le1\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow A\le1\)
Dấu "=" xảy ra khi x=y=1.
Vậy MaxA là 1, đạt được khi x=y=1.
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = 1, AC = 2; cạnh bên SA vuông góc với đáy và SA = 1. Gọi I là trung điểm của AC. Xét M là điểm thay đổi trên cạnh AB sao cho A M = x 0 < x < 1 và (P) là mặt phẳng đi qua M, song song với SA và IB. Thiết diện của hình chóp với mặt phẳng (P) có diện tích lớn nhất thì giá trị của x bằng.
A. 2 3
B. 3 4
C. 1 3
D. 1 2
\(\frac{\left(a-x\right)\left(a-y\right)}{a\left(a-b\right)\left(a-c\right)}+\frac{\left(b-x\right)\left(b-y\right)}{b\left(b-c\right)\left(b-a\right)}+\frac{\left(c-x\right)\left(c-y\right)}{c\left(c-a\right)\left(c-b\right)}\)
Tìm min của biểu thức biết a,b,c là các số thực dương khác nhau đôi một
trong đó x,y là 2 số dương thay đổi luôn có tổng là 1:
P/S bài này là em đố các bạn mong cô Linh Chi ko trả lời :D
Cho 2 số dương a,b. Các số dương x,y thay đổi sao cho \(\frac{a}{x}+\frac{b}{y}=1\). Tìm x,y để S=x+y đạt GTNN. Tìm GTNN đó theo a,b
Áp dụng bđt bunhia cho 2 bộ số \(\left(\frac{a}{x};\frac{b}{y}\right),\left(x;y\right)\)ta được
\(\left(\frac{a}{x}+\frac{b}{y}\right)\left(x+y\right)\ge\left(\sqrt{\frac{a}{x}.x}+\sqrt{\frac{b}{y}.y}\right)^2\)
\(\rightarrow x+y\ge\left(\sqrt{a}+\sqrt{b}\right)^2\)
\(MinS=\left(\sqrt{a}+\sqrt{b}\right)^{22}\)
Cho hình chóp S.ABC, lấy các điểm A', B', C' lần lượt thuộc các tia SA, SB, SC sao cho SA = aSA', SB = bSB' ,SC = cSC', trong đó a, b, c là các số thay đổi. Tìm mối liên hệ giữa a, b ,c để mặt phẳng (A'B'C') đi qua trọng tâm tam giác ABC ?
A. a + b +c =3
B. a + b +c =4
C. a + b +c =2
D. a + b +c =1
Đáp án A.
Hướng dẫn giải:
Nếu a = b = c = 1 thì SA = SA',SB = SB',SC = SC'
nên ( A B C ) ≡ ( A ' B ' C ' )
Dễ thấy (A'B'C') đi qua trọng tâm của tam giác ABC
⇒ a + b + c = 3 là đáp án đúng