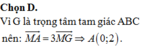Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có điểm M - 9 2 ; 3 2 là trung điểm của cạnh AB, điểm H(-2;4) và điểm I(-1;1) lần lượt là chân đường cao kẻ từ B và tâm đường tròn ngoại tiếp tam giác ABC. Tìm tọa độ điểm C, biết A có tung độ âm.
A. C(-4;5)
B. C(-5;2)
C. C(4;1)
D. D(-1;6)