Tìm tất cả các giá trị của m để hàm số y = l o g 2018 ( 2017 x - x - x 2 2 - m ) xác định với mọi x thuộc [ 0 ; + ∞ ) .
A. m>9
B. m<2
C. 0<m<1
D. m<1
Tìm tất cả các giá trị của tham số m để hàm số y = 1 3 x 3 - m x 2 + m + 6 + x + 2017 * có 5 điểm cực trị.
A. m < - 2 ∪ m > 5
B. m > -6
C.m > 0
D.m > 3
1,Tìm tất cả các giá trị của m để hàm số y=2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x=2. 2, Tìm tất cả các giá trị của m để hàm số y= x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x=2. 3, Tìm tất cả các giá trị của m để hàm số y=x^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu . 4, Tìm m để hso y=x^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu. Mọi người giúp em với ạ . Em cảm ơn ạ !
Cho hàm số y = f (x) có đồ thị như hình bên. Gọi S là tập tất cả các giá trị nguyên dương của tham số m để hàm số y = f x - 2018 + m có 5 điểm cực trị. Tổng tất cả các giá trị của tập S bằng
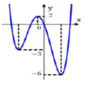
A. 9
B. 7
C. 12
D. 18
Cho đồ thị của hàm số y=f(x) như hình vẽ bên.Gọi S là tập hợp các giá trị nguyên dương của m để hàm số y = f x + 2018 + 1 3 m 2 có 5 điểm cực trị. Tổng tất cả các giá trị của các phần tử của S bằng
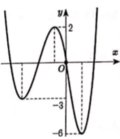
A. 7.
B. 6.
C. 5.
D. 9.
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Câu 2: Cho các hàm số bậc nhất \(y=\left(m-2\right)x+2\)
a. Tìm tất cả các giá trị của m để hàm số đã cho đồng biến trên R
b. Tìm tất cả các giá trị của m để đồ thị hàm số đã cho song song với đường thẳng \(y=5x+1\)
a) Để đồ thị hàm số \(y=\left(m-2\right)x+2\) đồng biến trên R.
=> \(m-2>0.\)
<=> \(m>2.\)
b) Đồ thị hàm số \(y=\left(m-2\right)x+2\) song song với đường thẳng \(y=5x+1.\)
=> \(m-2=5.\)
<=> \(m=7.\)
Câu 2
a) Để hs đã cho đồng biến trên R thì:
\(m-2>0\\ < =>m>2\)
b) Đề đths đã cho song song với đường thẳng \(y=5x+1\) thì:
\(m-2=5\\ < =>m=7\)
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) + m - 2018 = 0 có duy nhất một nghiệm.
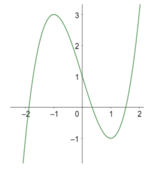
A. m ≤ 2015, m ≥ 2019.
B. 2015 < m < 2019.
C. m = 2015, m = 2019.
D. m < 2015, m > 2019.
Chọn D
Phương pháp:
Biến đổi phương trình về f(x) = 2018 - m và sử dụng tương giao đồ thị: Phương trình có duy nhất một nghiệm khi và chỉ khi đường thẳng y = 2018 - m cắt đồ thị hàm số y = f(x) tại duy nhất một điểm.
Cách giải:
Phương trình f(x) + m - 2018 = 0 ![]()
Đây là phương trình hoành độ giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = 2018 - m (có phương song song hoặc trùng với trục hoành).
Dựa vào đồ thị, ta có ycbt 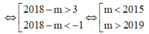
Cho hàm số y=f(x) xác định trên R và có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình f(x)+m-2018=0 có duy nhất một nghiệm.
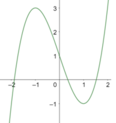
A. m ≤ 2015 , m ≥ 2019 .
B.2015<m<2019
C.m=2015,m=2019
D.m<2015,m>2019
Tìm tất cả các giá trị của tham số m để hàm số y = x 3 - 2 m x 2 + m 2 x + 2 đạt cực tiểu tại x= l
A. m= 1
B. m= 3
C. m = 1 ∨ m = 3
D. m= -1
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị