Giả sử đồ thị (C) của hàm số y = ( 2 ) x ln 2 cắt trục tung tại điểm A và tiếp tuyến của (C) tại A cắt trục hoành tại B. Tính diện tích S của tam giác AOB
A. S = 1 ln 2
B. S = ( 1 ln 2 ) 2
C. S = ( 1 ln 2 ) 3
D. S = ( 1 ln 2 ) 4
Giả sử đồ thị của hàm số y = f (x) là (C), khi tịnh tiến (C) theo Ox qua phải 1 đơn vị thì sẽ được đồ thị của hàm số:
![]()
![]()
![]()
![]()
Giả sử đồ thị của hàm số y = f (x) là (C), khi tịnh tiến (C) theo Oy xuống dưới 1 đơn vị thì sẽ được đồ thị của hàm số:
![]()
![]()
![]()
![]()
Giả sử đồ thị của hàm số y = x 4 - 2 x 2 - 1 là C , khi tịnh tiến C theo O y lên trên 1 đơn vị thì sẽ được đồ thị của hàm số
![]()
![]()
![]()
![]()
Chọn A.
Đặt f ( x ) = x 4 - 2 x 2 - 1 thì khi tịnh tiến (C) theo O y lên trên 1 đơn vị thì sẽ được đồ thị của y = f ( x ) + 1 = x 4 - 2 x 2 .
Cho hàm số y = x 3 - 3 x + 1 có đồ thị là (C).Giả sử (d) là tiếp tuyến của (C) tại điểm có hoành độ x = 2, đồng thời (d) cắt đồ thị (C) tại N, tìm tọa độ N.
A. N(1;-1)
B. N(2;3)
C. N(-4;-51)
D. N(3;19)
- Tiếp tuyến (d) tại điểm M của đồ thị (C) có hoành độ x 0 = 0 ⇒ y 0 = 3 .
- Ta có:
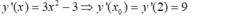
- Phương trình tiếp tuyến (d) tại điểm M của đồ thị (C) là:
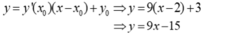
- Xét phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d là nghiệm phương trình :
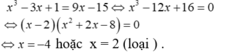
- Với x = -4 thì y = 9.(-4) – 15 = -51.
- Vậy N(- 4 ; -51) là điểm cần tìm.
Chọn C.
Giả sử đồ thị của hàm số y = x 4 - 2 x 2 - 1 là ( C ) , khi tịnh tiến ( C ) theo O x qua trái 1 đơn vị thì sẽ được đồ thị của một hàm số trong 4 hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
![]()
![]()
![]()
![]()
Chọn D.
Đặt f ( x ) = x 4 - 2 x 2 - 1 thì khi tịnh tiến (C) theo O x qua trái 1 đơn vị thì sẽ được đồ thị của y = f ( x + 1 ) = ( x + 1 ) 4 - 2 ( x + 1 ) 2 - 1 .
Hình vẽ bên là đồ thị (C) của hàm số y = f(x).
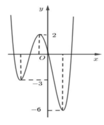
Giả sử m là tham số thực nhận giá trị thuộc nửa khoảng (0;3]. Hỏi hàm số y = f x - 1 + m có thể có bao nhiêu điểm cực trị
A. 5 hoặc 7 điểm
B. 3 điểm
C. 6 hoặc 8 điểm
D. 4 điểm
Chọn A.
Phương pháp : Sử dụng các phép suy đồ thị.

Lấy đối xứng phần bên dưới trục hoành qua trục hoành và bỏ phần bên dưới trục hoành.
Do đó:

C3: Giả sử các biểu thức đều có nghĩa. Với giá trị nào của a thì hai phân thức x/x+1 và ax^2-ax/x^2-1 bằng nhau:
A. -1 B. 1 C. 2 D.3
C5: Hàm số nào sau đây là hàm số bậc nhất
A. y=2x-1 B.y=2 C.y=x^2+x+1 D. y=2/x
C6: Đồ thị hàm số y=x+2 đi qua điểm có tọa độ nào sau đây
A. (0;-2) B.(1;3) C.(-1;0) D.(0;0)
C8: Giá trị m để đường thẳng y=(m-1)x+3 với ( m khác 1) song song với đường thẳng y=x là ?
A. m=0 B. m=1 C. m=2 D.không có giá trị của m
C9: Tổng số cạnh bên và cạnh đáy của hình chóp tam giác đều là
A.4 B.6 C.8 D.10
C10 S xung quanh hình chóp đều =?
A,tích nửa chu vi đáy và đường cao của hình chóp
B. Tích nửa chu vi đáy và độ dài trung đoạn
C. Tích chu vi đáy và độ dài trung đoạn
D. Tổng chu vi đáy và trung đoạn
C11 : Tứ giác ABCD có C=50 độ ; D=60 độ; A:B=3:2. Số đo B bằng?
A 50 độ B.100 độ C.150 độ D.200 độ
C12 :phát biểu nào sau đây là sai?
A. tứ giác có 4 cạnh =nhau và 4 góc = nhau là hình vuông
B. tứ giác có 2 dường chéo bằng nhau là hình bình hành
C. tứ giác có 4 cạnh bằng nhau là hình thoi
D. Tứ giác có 4 góc = nhau là hình chữ nhật
Câu 3: B
Câu 5: A
Câu 6: B
Câu 8: C
Câu 9: B
Câu 10:B
Câu 11: B
Câu 12: B
Giả sử F(x) là nguyên hàm của hàm số f(x)=4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là
A. (0;-1)
B. 5 2 ; 8
C. 0 ; - 1 v à 5 2 ; 9
D. 5 2 ; 9
f ( x ) = 4 x - 1 ⇒ F ( x ) = ∫ f ( x ) d x = 2 x 2 - x + C
Phương trình hoành độ giao điểm của đồ thị hàm số F(x) và f(x) là:
2 x 2 - x + C = 4 x - 1 ⇔ 2 x 2 - 5 x + C + 1 = 0 ( * )
Do hai đồ thị hàm số trên cắt nhau tại một điểm trên trục tung nên x=0 là nghiệm của (*)
⇔ C + 1 = 0 ⇔ C = - 1
Với C=-1: Phương trình(*)
⇔ 2 x 2 - 5 x = 0 ⇔ [ x = 0 x = 5 2
Tọa độ các điểm chung của hai đồ thị hàm số trên là: (0;-1) và 5 2 ; 9
Chọn đáp án C.
Giả sử F(x) là nguyên hàm của hàm số f(x)=4x-1. Đồ thị hàm số F(x) và f(x) cắt nhau tại một điểm trên trục tung. Tọa độ các điểm chung của hai đồ thị hàm số trên là:
![]()
![]()
![]()
![]()
Phương pháp:
+) Sử dụng các công thức nguyên hàm cơ bản
xác định hàm số F(x).
+) Giải phương trình hoành độ giao điểm.
Cách giải:
![]()
Phương trình hoành độ giao điểm của
đồ thị hàm số F(x) và f(x) là :
![]()
Do hai đồ thị hàm số trên cắt nhau tại một
điểm trên trục tung nên x=0 là nghiệm của (*)
![]()
![]()
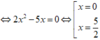
Tọa độ các điểm chung của hai đồ thị
hàm số trên là:
![]()
Giả sử hàm số y = f ( x ) có đạo hàm là hàm số y=f'(x) có đồ thị được cho như hình vẽ dưới đây và f 0 + f 1 - 2 f 2 = f 4 - f 3 Tìm giá trị nhỏ nhất m của hàm số y = f ( x ) trên [0;4].
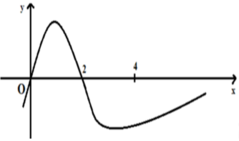
A. m = f 4
B. m = f 0
C. m = f 2
D. m = f 1