Tổng tất cả các điểm cực đại của hàm số y=cosx+2017 nằm trong khoảng [ 0 ; 2 π ] là
A. 2 π
B. π 2
C. π
D. 3 π 2
Những câu hỏi liên quan
Cho hàm số
y
2
x
3
+
3
m
−
1
x
2
+
6
m
−
2
x
−
1
với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng (-2;3) A.
m...
Đọc tiếp
Cho hàm số y = 2 x 3 + 3 m − 1 x 2 + 6 m − 2 x − 1 với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng (-2;3)
A. m ∈ − 1 ; 4 \ 3 .
B. m ∈ 3 ; 4 .
C. m ∈ 1 ; 3 .
D. m ∈ − 1 ; 4 .
Cho hàm số
y
2
x
3
+
3
m
-
1
x
2
+
6
m
-
2
x
-
1
với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng (-2; 3) . A. m
∈...
Đọc tiếp
Cho hàm số y = 2 x 3 + 3 m - 1 x 2 + 6 m - 2 x - 1 với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có điểm cực đại và điểm cực tiểu nằm trong khoảng (-2; 3) .
A. m ∈ - 1 ; 3 ∪ 3 ; 4
B. (1; 3)
C. (3; 4)
D. (-1; 4)
Ta có
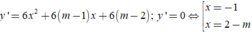
Để hàm số có hai cực trị kh y’=0 có hai nghiệm phân biệt
⇔ 2 - m ≠ - 1 ⇔ m ≠ 3
● Nếu -1<2-m hay m<3,
ycbt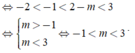 
● Nếu 2-m<-1 hay m>3, ycbt
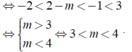
Vậy m ∈ - 1 ; 3 ∪ 3 ; 4
Chọn A.
Đúng 0
Bình luận (0)
Cho hàm số \(y=2x^3+3\left(m-1\right)x^2+6\left(m-2\right)x-1\) với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có điểm cực đại và cực tiểu nằm trong khoảng (-2;3)
Tính tổng tất cả các giá trị thực của tham số m để hàm số y x3-3mx2+ 3( m2-1) x- m3+ m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng
2
lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O. A. -4 B. -5 C. -6. D. -7
Đọc tiếp
Tính tổng tất cả các giá trị thực của tham số m để hàm số y= x3-3mx2+ 3( m2-1) x- m3+ m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O.
A. -4
B. -5
C. -6.
D. -7
Ta có y’ = 3x2- 6mx + 3( m2-1).
Hàm số đã cho có cực trị thì phương trình y’ =0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nghiệm phân biệt ⇔ ∆ = 1 > 0 , ∀ m
Khi đó, điểm cực đại A( m-1; 2-2m) và điểm cực tiểu B( m+1; -2-2m)
Ta có
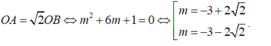
Tổng hai giá trị này là -6.
Chọn C.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
-
3
m
x
2
+
3
(
m
2
-
1
)
x
-...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + 3 ( m 2 - 1 ) x - m 3 + m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O
A. m = - 3 - 2 2 h o ặ c m = - 1
B. m = - 3 + 2 2 h o ặ c m = - 1
C. m = - 3 + 2 2 h o ặ c m = - 3 - 2 2 .
D. m = - 3 + 2 2
Chọn C
Ta có y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 )
Hàm số (1) có cực trị thì PT y ' = 0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nhiệm phân biệt
Khi đó, điểm cực đại A ( m - 1 ; 2 - 2 m ) và điểm cực tiểu B ( m + 1 ; - 2 m )
Ta có O A = 2 O B ⇔ m 2 + 6 m + 1 = 0
Đúng 0
Bình luận (0)
Cho hàm số yx+sin2 x+2017. Tìm tất cả các điểm cực tiểu của hàm số A.
x
-
π
/
3
+
k
π
,
k
∈
Z
B.
x
-
π
/
3
+
k
2
π
,
k
∈
Z
C.
x
π
/...
Đọc tiếp
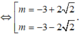
Cho hàm số y=x+sin2 x+2017. Tìm tất cả các điểm cực tiểu của hàm số
A. x = - π / 3 + k π , k ∈ Z
B. x = - π / 3 + k 2 π , k ∈ Z
C. x = π / 3 + k 2 π , k ∈ Z
D. x = π / 3 + k π , k ∈ Z
Tìm tất cả các giá trị thực của tham số m để hàm số
y
cos
x
−
2
cos
x
−
m
nghịch biến trên khoảng
0
;
π
2
A. m 2 B.
m
≤
0
hoặc
1...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = cos x − 2 cos x − m nghịch biến trên khoảng 0 ; π 2
A. m > 2
B. m ≤ 0 hoặc 1 ≤ m < 2
C. m ≤ 2
D. m ≤ 0
Tìm tất cả các giá trị thực của tham số m để hàm số
y
cos
x
-
2
cos
x
-
m
đồng biến trên khoảng (0;
π
2
). A.. B.. C. hoặc . D..
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = cos x - 2 cos x - m đồng biến trên khoảng (0; π 2 ).
A.
.
B.
.
C.
hoặc 
.
D.
.
Chọn D
Đặt 
, 
thì 
. Ta có:
.
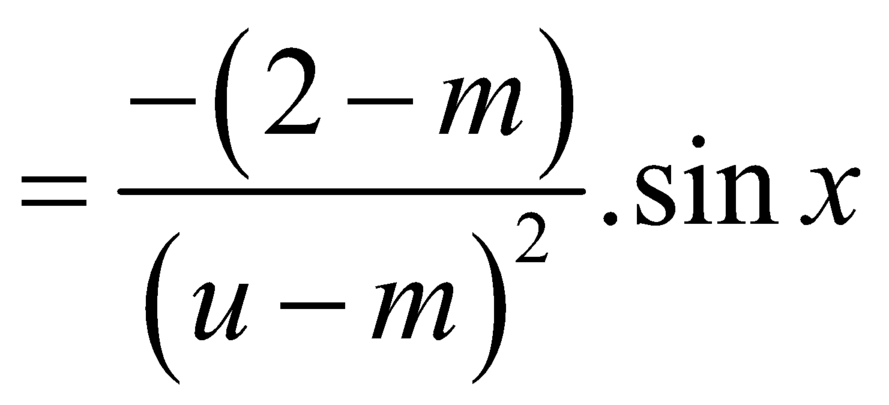Vì 
nên ycbt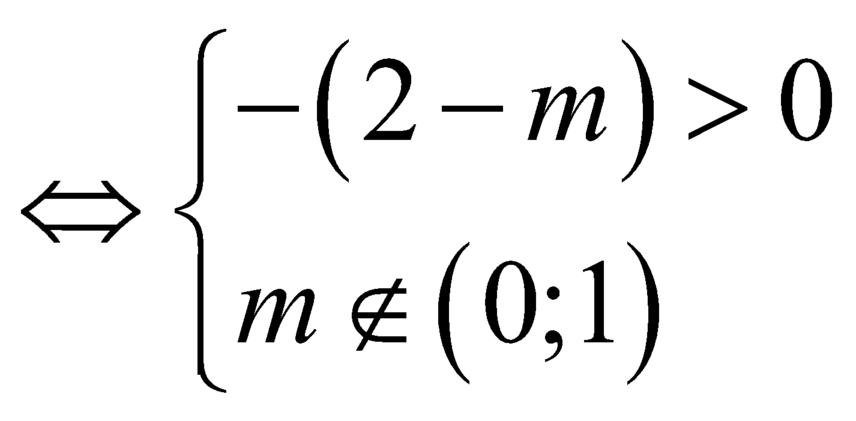
.
Đến đây giải được: 
.
Đúng 0
Bình luận (0)
Có tất cả bao nhiêu giá trị nguyên của tham số thực m để đồ thị của hàm số
y
x
3
3
−
x
2
2
m
+
2
+
2
m
x
+
1
có một điểm cực đại và một điểm cực tiểu đồng thời chúng nằm về cùng một phía so với đường thẳng...
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của tham số thực m để đồ thị của hàm số y = x 3 3 − x 2 2 m + 2 + 2 m x + 1 có một điểm cực đại và một điểm cực tiểu đồng thời chúng nằm về cùng một phía so với đường thẳng d : x + y − 1 = 0
A. 3
B. 4
C. 5
D. 6
