Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông BA = BC = a, cạnh bên A A ' = a 2 . M là trung điểm của BC. Khoảng cách giữa AM và B'C là:
A. a 2 2 .
B. a 3 3 .
C. a 5 5 .
D. a 7 7 .
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông BA=BC=a, cạnh bên AA'= a 2 , M là trung điểm của BC. Khoảng cách giữa AM và B'C là:
A . a 2 2
B . a 3 3
C . a 5 5
D . a 7 7
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông BA=BC=a, cạnh bên AA'=a 2 , M là trung điểm của BC. Khoảng cách giữa AM và B' C là:
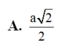
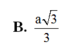
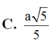
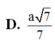
Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông BA=BC=a, cạnh bên A A ' = a 2 . M là trung điểm của BC. Khoảng cách giữa AM và B'Clà
A. a 2 2
B. a 3 3
C. a 5 5
D. a 7 7
Đáp án D
Chọn hệ trục tọa độ như hình vẽ
A 0 ; a ; a 2 , M a 2 ; 0 ; a 2 , B ' 0 ; 0 ; 0 ; , C a ; 0 ; a 2 A M → a 2 ; - a ; 0 , B ' C → a ; 0 ; a 2 ⇒ A M → , B ' C → = - a 2 2 ; - a 2 2 ; a 2 B ' M → a 2 ; 0 ; a 2
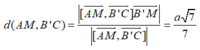

Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông BA = BC = a, cạnh bên AA ' = a 2 , M là trung điểm của BC. Khoảng cách giữa AM và B'C là:
A. a 2 2
B. a 3 3
C. a 5 5
D. a 7 7
Cho lăng trụ đứng A B C . A ' B ' C ' có đáy A B C là tam giác vuông tại A ; B C = 2 a ; A B C = 30 0 . Biết cạnh bên của lăng trụ bằng 2 a 3 . Thể tích khối lăng trụ là:
A. a 3 3
B. 6 a 3
C. 3 a 3
D. 2 a 3 3
Ta có:
• A C = B C . sin 30 0 = a ; A B = B C . cos 30 0 = a 3 .
• V A B C . A ' B ' C ' = B B ' . S A B C = 2 a 3 . 1 2 . a 3 . a = 3 a 3 .

Cho lăng trụ đứng tam giác ABC.A'B'C' có đáy ABC là tam giác vuông, AB=BC=a, cạnh bên \(AA'=a\sqrt{2}\). Gọi M là trung điểm cạnh BC. Tính theo a thể tích của khối lăng trụ ABC.A'B'C' và khoảng cách giữa 2 đường thẳng AM, B'C
Từ giả thiết ta suy ra tam giác ABC là tam giác vuông cân tại B
Thể tích của khối lăng trụ là \(V_{ABC.A'B'C'}=AA'.BC=a\sqrt{2.}\frac{1}{2}a^2=\frac{\sqrt{2}}{2}a^3\)
Gọi E là trung điểm của BB'. Khi đó mặt phẳng (AME) song song với B'C nên khoảng cách giữa 2 đường thẳng AM, B'C bằng khoảng cách giữa B'C và mặt phẳng (AME)
Nhận thấy, khoảng cách từ B đến mặt phẳng (AME) bằng khoảng cách từ C đến mặt phẳng (AME)
Gọi h là khoảng cách từ B đến mặt phẳng (AME). Do đó tứ diện BAME có BA, BM, BE đôi một vuông góc với nhau nên :
\(\frac{1}{h^2}=\frac{1}{BA^2}+\frac{1}{BM^2}+\frac{1}{BE^2}\Rightarrow\frac{1}{h^2}=\frac{1}{a^2}+\frac{4}{a^2}+\frac{2}{a^2}=\frac{7}{a^2}\)
\(\Rightarrow h=\frac{a\sqrt{7}}{7}\)
Vậy khoảng cách giữa 2 đường thẳng B'C và AM bằng \(\frac{a\sqrt{7}}{7}\)
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông BA=BC=a, cạnh bên A A ' = a 2 , M là trung điểm của BC. Khoảng cách giữa AM và B' C là:
A. a 2 2
B. a 3 3
C. a 5 5
D. a 7 7
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Cạnh bên AA'=a 2 . Thể tích khối lăng trụ ABC.A'B'C' là:
A. V = a 3 6 4
B. V = a 3 6 2
C. V = a 3 6 12
D. V = a 6 4
Cho hình lăng trụ đứng A B C . A ' B ' C ' có đáy là A B C là tam giác vuông B A = B C = a , cạnh bên AA ' = a 2 .Gọi M là trung điểm của B C . Tính khoảng cách giữa hai đường thẳng A M , B ' C ' .
A. d A M , B ' C = a 7 7
B. d A M , B ' C = a 2 2
C. d A M , B ' C = a 3 3
D. d A M , B ' C = a 5 5
Đáp án là A
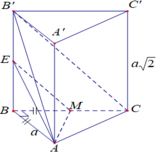
Gọi E là trung điểm của B B ' . Khi đó B ' C / / A M E ⇒ d A M ; B ' C = d B ' C ; A M E .
Mặt khác d B ; A M E = d C ; A M E . Gọi h = d B ; A M E
Vì tứ diện B A M E có B A ; B M ; B E đôi một vuông góc với nhau.
⇒ 1 h 2 = 1 B A 2 + 1 B M 2 + 1 B E 2 ⇒ 1 h 2 = 1 a 2 + 4 a 2 + 2 a 2 = 7 a 2 ⇒ h = a 7 7 ⇒ d B ' C ; A M = a 7 7 .