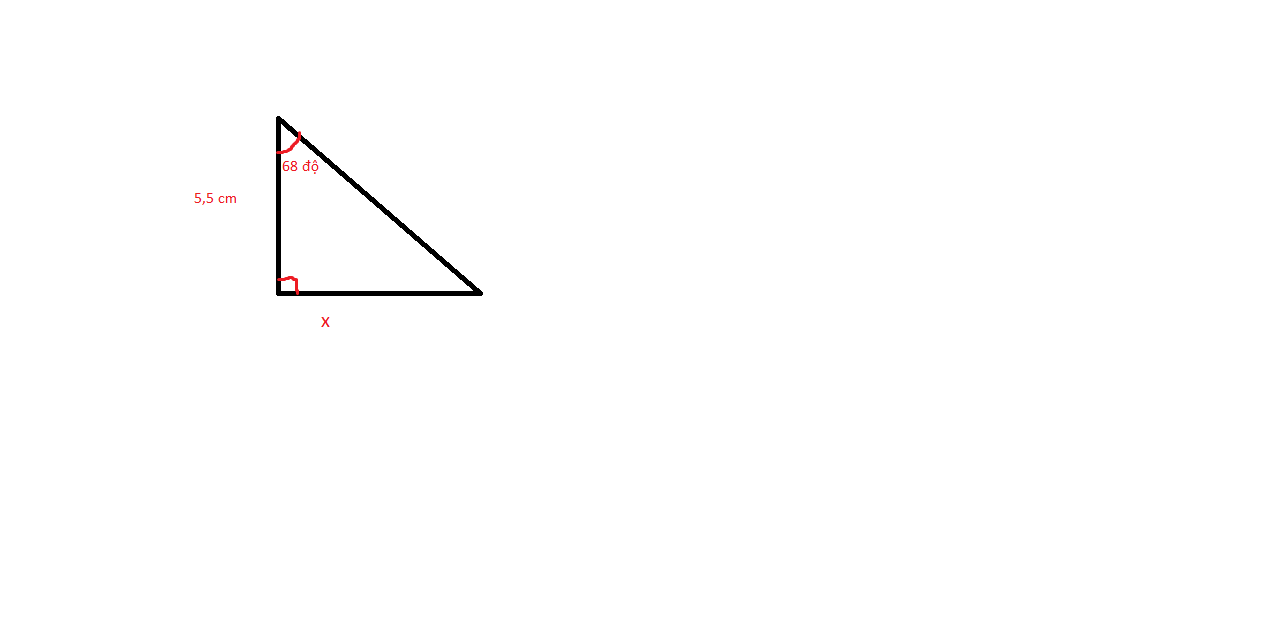 tìm độ dài x trong hình
tìm độ dài x trong hình

Những câu hỏi liên quan
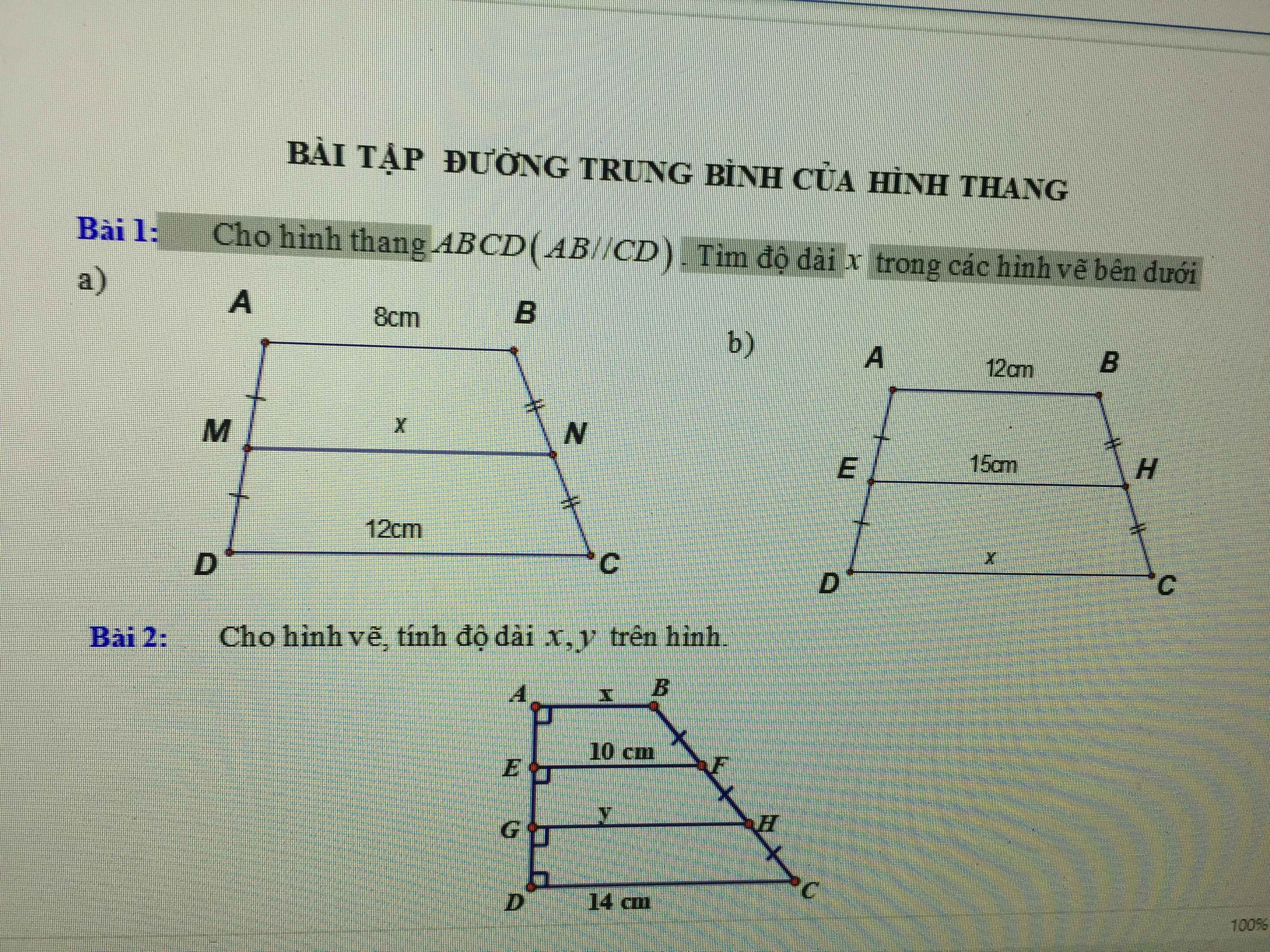
Cho hình thang ABCD(AB//CD). Tìm độ dài x trong các hình vẽ bên dưới
Cho tam giác ABC có AD là phân giác trong của góc A. Tìm x trong hình vẽ sau với độ dài cho sẵn trong hình.
vì AD là phân giác góc A của tam giác BAC
=>\(\dfrac{AB}{AC}=\dfrac{BD}{DC}< =>\dfrac{x}{5}=\dfrac{5,1}{3}=>x=\dfrac{5.5,1}{3}=8,5cm\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có AD là phân giác trong của góc A. Tìm x trong hình vẽ sau với độ dài cho sẵn trong hình.
△ABC có AD là đường phân giác nên:
\(\dfrac{AB}{AC}=\dfrac{BD}{DC}\)(tích chất đường phân giác trong tam giác)
\(\dfrac{x}{5}=\dfrac{5,1}{3}\)
x = \(\dfrac{5,1.5}{3}\)=8,5 (cm)
Đúng 1
Bình luận (0)
Cho hình thang ABCD(AB//CD). Tìm độ dài x trong các hình vẽ bên dưới

Giải chi tiết giúp mình nha
Trong hình bên có DE song song FH song song BC. Tìm các độ dài x, y
BẠN ƠI KHÔNG CÓ HÌNH
Cho hình vuông ABCD có tâm O và có các cạnh bằng a (hình 16)
a) Tìm trong hình hai vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\)
b) Tìm trong hình hai vectơ đối nhau và có độ dài bằng \(a\sqrt 2\)
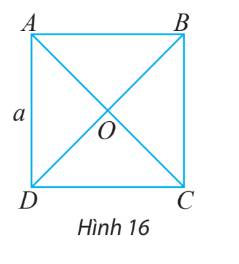
a) \(AC = BD = \sqrt {A{D^2} + D{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow AO = OC = BO = OD = \frac{{a\sqrt 2 }}{2}\)
Suy ra các cặp vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\) là:
\(\overrightarrow {AO} \)và \(\overrightarrow {OC} \); \(\overrightarrow {CO} \) và \(\overrightarrow {OA} \); \(\overrightarrow {DO} \) và \(\overrightarrow {OB} \); \(\overrightarrow {OD} \) và \(\overrightarrow {BO} \)
b) Trong hình chỉ có 2 đoạn thẳng AC và BD có độ dài là \(a\sqrt 2\).
Do đó hai vectơ đối nhau và có độ dài bằng \(a\sqrt 2\) là:
\(\overrightarrow {AC} \)và \(\overrightarrow {CA} \); \(\overrightarrow {BD} \) và \(\overrightarrow {DB} \).
Đúng 1
Bình luận (0)
Cho hình vuông cạnh 2x và bên trong là hình chữ nhật có độ dài hai cạnh là x và 3 (Hình 5). Tìm đa thức theo biến x biểu thị diện tích của phần được tô màu xanh.
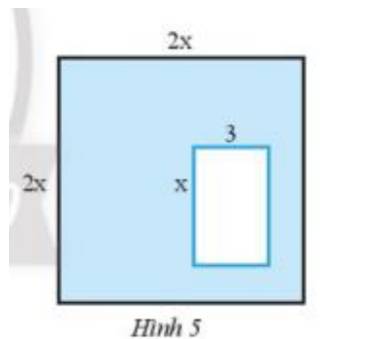
Diện tích hình vuông là : \(2x.2x = 4{x^2}\)
Diện tích hình chữ nhật là : \(3.x = 3x\)
Diện tích phần cần tìm là : \(4{x^2} - 3x\)
Đúng 0
Bình luận (0)
Tìm độ dài x trên hình 127.
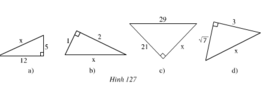
- Hình a
Áp dụng định lí Pi-ta-go ta có:
x2 = 122 + 52 = 144 + 25 = 169 ⇒ x = 13
- Hình b
Ta có: x2 = 12 + 22 = 1 + 4 = 5
⇒ x = √5
- Hình c
Theo định lí Pi-ta-go 292 = 212 + x2
Nên x2 = 292 - 212 = 841 - 441 = 400
⇒ x = 20
- Hình d
Theo định lí Pi-ta-go ta có:
x2 = (√7)2 + 32 = 7 + 9 = 16
⇒ x = 4
Đúng 0
Bình luận (0)
Tìm độ dài \(x\) trên Hình 13.
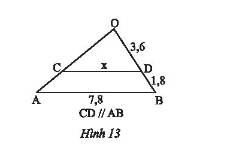
Trong tam giác \(OAB\) có \(CD//AB\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{OD}}{{OB}} = \frac{{CD}}{{AB}}\) mà \(OB = OD + DB = 3,6 + 1,8 = 5,4\)
Suy ra, \(\frac{{3,6}}{{5,4}} = \frac{x}{{7,8}} \Rightarrow x = \frac{{3,6.7,8}}{{5,4}} = 5,2\).
Vậy \(x = 5,2\).
Đúng 1
Bình luận (0)













