Tìm điều kiện của biến để giá trị của phân thức xác định: x 2 x + z

Những câu hỏi liên quan
1.Cho biểu thức C x³/x²-4 - x/x-2 - 2/x+2 a,tìm giá trị của biến để biểu thức được xác địnhb,Tìm x để C0c,Tìm giá trị nguyên của x để C nhận giá trị dương 2,cho P (2+x/2-x + 4x²/x²-4 - 2-x/2+x): x²-3x/2x²-x³a,Tìm điều kiện của x để giá trị của P được xác định B, rút gọn Pc,Tính giá trị P với |x-5|2d,Tìm x để P03,cho biểu thức B [x+1/2x-2 + 3/x²-1 - x+3/2x+2]. 4x²-4/5a,Tìm điều kiện của x để giá trị biểu thức được xác định b,CMR khi giá trị của biểu thức không phụ thuộc vào giá trị của biến x?...
Đọc tiếp
1.Cho biểu thức C = x³/x²-4 - x/x-2 - 2/x+2
a,tìm giá trị của biến để biểu thức được xác định
b,Tìm x để C=0
c,Tìm giá trị nguyên của x để C nhận giá trị dương
2,cho P = (2+x/2-x + 4x²/x²-4 - 2-x/2+x): x²-3x/2x²-x³
a,Tìm điều kiện của x để giá trị của P được xác định
B, rút gọn P
c,Tính giá trị P với |x-5|=2
d,Tìm x để P<0
3,cho biểu thức B = [x+1/2x-2 + 3/x²-1 - x+3/2x+2]. 4x²-4/5
a,Tìm điều kiện của x để giá trị biểu thức được xác định
b,CMR khi giá trị của biểu thức không phụ thuộc vào giá trị của biến x?
4,Cho phân thức C = 3x²-x/9x²-6x+1
a, tìm điều kiện xác định phân thức
b,tính giá trị phân thức tại x=-8
c,Tìm x để giá trị của phân thức nhận giá trị dương
1.a)\(\frac{x^3}{x^2-4}-\frac{x}{x-2}-\frac{2}{x+2}\)
\(=\frac{x^3}{\left(x+2\right)\left(x-2\right)}-\frac{x}{x-2}-\frac{2}{x+2}\)
Để biểu thức được xác định thì:\(\left(x+2\right)\left(x-2\right)\ne0\)\(\Rightarrow x\ne\pm2\)
\(\left(x+2\right)\ne0\Rightarrow x\ne-2\)
\(\left(x-2\right)\ne0\Rightarrow x\ne2\)
Vậy để biểu thức xác định thì : \(x\ne\pm2\)
b) để C=0 thì ....
Đúng 1
Bình luận (0)
1, c , bn Nguyễn Hữu Triết chưa lm xong
ta có : \(/x-5/=2\)
\(\Rightarrow\orbr{\begin{cases}x-5=2\\x-5=-2\end{cases}}\Rightarrow\orbr{\begin{cases}x=7\\x=3\end{cases}}\)
thay x = 7 vào biểu thứcC
\(\Rightarrow C=\frac{4.7^2\left(2-7\right)}{\left(7-3\right)\left(2+7\right)}=\frac{-988}{36}=\frac{-247}{9}\)KL :>...
thay x = 3 vào C
\(\Rightarrow C=\frac{4.3^2\left(2-3\right)}{\left(3-3\right)\left(3+7\right)}\)
=> ko tìm đc giá trị C tại x = 3
Đúng 0
Bình luận (0)
chết mk nhìn nhầm phần c bài 2 :
\(2,\left(\frac{2+x}{2-x}+\frac{4x^2}{x^2-4}-\frac{2-x}{2+x}\right):\frac{x^2-3x}{2x^2-x^3}\)
Để P xác định
\(\Rightarrow2-x\ne0\Rightarrow x\ne2\)
\(2+x\ne0\Rightarrow x\ne-2\)
\(x^2-4\ne0\Rightarrow x\ne0\)
\(x^2-3x\ne0\Rightarrow x\ne3\)
b, \(P=\left(\frac{2+x}{2-x}+\frac{4x^2}{\left(2+x\right)\left(2-x\right)}+\frac{2-x}{2+x}\right):\frac{x\left(x-3\right)}{x^2\left(2-x\right)}\)
\(P=\left[\frac{4+4x+x^2}{\left(2-x\right)\left(2+x\right)}-\frac{4x^2}{\left(2+x\right)\left(2-x\right)}-\frac{4-4x+x^2}{\left(2+x\right)\left(2-x\right)}\right].\frac{x\left(2-x\right)}{x-3}\)
\(P=\left[\frac{8x-4x^2}{\left(2-x\right)\left(2+x\right)}\right].\frac{x\left(2-x\right)}{x-3}=\frac{4x\left(2-x\right)}{\left(2-x\right)\left(2+x\right)}.\frac{x\left(2-x\right)}{x-3}\)
\(P=\frac{4x^2\left(2-x\right)}{\left(x-3\right)\left(2+x\right)}\)
d, ĐỂ \(p=\frac{8x^2-4x^3}{x^2-x-6}< 0\)
\(TH1:8x^2-4x^3< 0\)
\(\Rightarrow8x^2< 4x^3\)
\(\Rightarrow2< x\Rightarrow x>2\)
\(TH2:x^2-x-6< 0\Rightarrow x^2< x+6\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho biểu thức B=[ x+1/ 2x-2 +3/x2 -1 -x+3/2x+2] .2x2 -2/5
a, tìm điều kiện của biến để phân thức xác định
b, c/m rằng khi giá trị của biểu thức xác định thì nó không phụ thuộc vào biến x ?
Cho phân thức :\(\dfrac{3x+3}{x^2-1}\)
a) Tìm điều kiện của x để giá trị của phân thức được xác định . Tìm giá trị của x để phân thức có giá trị bằng -2
b) Tìm giá trị của x để phân thức có giá trị là số nguyên
\(a,ĐK:x^2-1=\left(x-1\right)\left(x+1\right)\ne0\Leftrightarrow x\ne\pm1\\ \dfrac{3x+3}{x^2-1}=\dfrac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{3}{x-1}=2\\ \Leftrightarrow x-1=\dfrac{3}{2}\Leftrightarrow x=\dfrac{5}{2}\left(tm\right)\\ b,\dfrac{3}{x-1}\in Z\\ \Leftrightarrow x-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow x\in\left\{-2;0;2;4\right\}\left(tm\right)\)
Đúng 0
Bình luận (0)
Giả sử
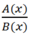
là một phân thức của biến x. Hãy nêu điều kiện của biến để giá trị của phân thức được xác định.
Phân thức được xác định khi biến x thỏa mãn B(x) ≠ 0.
Đúng 0
Bình luận (0)
2/ Cho phân thức: x^2+6x+9/x+3
a/ Tìm điều kiện của x để giá trị của phân thức được xác định ?
b/ Rút gọn phân thức
c/ Tìm giá trị của x để giá trị của phân thức bằng -5
d/ Tính giá trị của phân thức tại x =1/2
Bài 1: Cho phân thức: 3x2+6x+12x3−83x2+6x+12x3−8a,Tìm điều kiện của x để phân thức đã cho được xác địnhb, Rút gọn phân thứcc, Tính giá trị của phân thức sau khi rút gọn với x 4001200040012000Bài 2: Cho phân thức: x2−10x+25x2−5xx2−10x+25x2−5xa, Tìm giá trị của x để phân thức bằng 0b, Tìm x để giá trị của phân thức bằng 5252c, Tìm x nguyên để phân thức có giá trị nguyênBài 3: Cho biểu thức: (x+12x−2+3x2−1−x+32x+2)(4x2−45)(x+12x−2+3x2−1−x+32x+2)(4x2−45)a, Tìm điều kiện của x để giá trị của biểu th...
Đọc tiếp
Bài 1: Cho phân thức: 3x2+6x+12x3−83x2+6x+12x3−8
a,Tìm điều kiện của x để phân thức đã cho được xác định
b, Rút gọn phân thức
c, Tính giá trị của phân thức sau khi rút gọn với x = 4001200040012000
Bài 2: Cho phân thức: x2−10x+25x2−5xx2−10x+25x2−5x
a, Tìm giá trị của x để phân thức bằng 0
b, Tìm x để giá trị của phân thức bằng 5252
c, Tìm x nguyên để phân thức có giá trị nguyên
Bài 3: Cho biểu thức: (x+12x−2+3x2−1−x+32x+2)(4x2−45)(x+12x−2+3x2−1−x+32x+2)(4x2−45)
a, Tìm điều kiện của x để giá trị của biểu thức được xác định
b, CMR: Khi giá trị của biểu thức được xác định thì nó không phụ thuộc vào giá trị của biến x
x2−10x+25x2−5x=(x−5)2x(x−5)=x−5x" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">x2−10x+25x2−5x=(x−5)2x(x−5)=x−5x
x−5x" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">x−5x phải có giá trị nguyên.
x+12x−2+3x2−1−x+32x+2)⋅(4x2−45)" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">x+12x−2+3x2−1−x+32x+2)⋅(4x2−45)
x+12(x−1)+3(x−1)(x+1)−x+32(x+1))⋅2(2x2−2)5" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">x+12(x−1)+3(x−1)(x+1)−x+32(x+1))⋅2(2x2−2)5
(x+1)2+6−(x−1)(x+3)2(x−1)(x+1)⋅2⋅2(x2−1)5" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">(x+1)2+6−(x−1)(x+3)2(x−1)(x+1)⋅2⋅2(x2−1)5
(x+1)2+6−(x2+3x−x−3)(x−1)(x+1)⋅2(x−1)(x+1)5" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">(x+1)2+6−(x2+3x−x−3)(x−1)(x+1)⋅2(x−1)(x+1)5
25" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">25
25" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">25
25" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">25
2(x+1)25+185−25x2−45x" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline-table; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">2(x+1)25+185−25x2−45x
2(x2+2x+1)5+185−25x2−45x" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">2(x2+2x+1)5+185−25x2−45x
2x2+4x+25+185−25x2−45x" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">2x2+4x+25+185−25x2−45x
2x2+4x+2+185−25x2−45x" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">2x2+4x+2+185−25x2−45x
2x2+4x+205−25x2−45x" role="presentation" style="border:0px; box-sizing:border-box; direction:ltr; display:inline; float:none; line-height:normal; margin:0px; max-height:none; max-width:none; min-height:0px; min-width:0px; overflow-wrap:normal; padding:0px; position:relative; white-space:nowrap; word-spacing:normal" class="MathJax">2x2+4x+205−25x2−45x
c) tự làm, đkxđ: x≠1;x≠−1
a) Tìm điều kiện của biến x để giá trị của biểu thức xác định. b) Tính giá trị của biểu thức với x=20040
a: ĐKXĐ: \(x\notin\left\{0;10;-10\right\}\)
Đúng 0
Bình luận (0)
Cho biểu thức:
P
x
2
+
2
x
2
x
+
12
+
x
−
6
x
+
108
−
6
x
2...
Đọc tiếp
Cho biểu thức: P = x 2 + 2 x 2 x + 12 + x − 6 x + 108 − 6 x 2 x ( x + 6 ) .
a) Tìm điều kiện của biến x để giá trị của biểu thức đuợc xác định;
b) Rút gọn phân thức;
c) Tìm giá trị của x để giá trị của biểu thức bằng 3 2
d) Tìm giá trị của x để giá trị của biểu thức bằng - 9 2
e) Tìm giá trị của x để giá trị của biểu thức bằng 1.
a) Tìm được x ≠ -6 và x ≠ 0.
b) Gợi ý: x 3 + 4 x 2 - 6x + 36 = (x + 6) ( x 2 - 2x + 6)
Tìm được P = x 2 − 2 x + 6 2 x
c) Ta có P = 3 2 ⇔ x 2 − 5 x + 6 = 0 . Từ đó tìm được x = 2 hoặc x = 3 (TMĐK).
d) Tương tự câu c, tìm được x = -6 (KTM) hoặc x = -1 (TM)
e) P = 1 Þ x 2 ‑ - 4x + 6= 0 Û ( x - 2 ) 2 + 2 = 0 (vô nghiệm)
Vì ( x - 2 ) 2 + 2 ≥ 2 > 0 với mọi x. Do vậy x ∈ ∅ .
Đúng 0
Bình luận (0)
Baøi 9: Cho phân thức : P a) Tìm điều kiện của x để P xác định. b) Tìm giá trị của x để phân thức bằng 1 c) Tìm x để giá trị của phân thức nhận giá trị dương
Đọc tiếp
Baøi 9: Cho phân thức : P =
a) Tìm điều kiện của x để P xác định.
b) Tìm giá trị của x để phân thức bằng 1
c) Tìm x để giá trị của phân thức nhận giá trị dương
a) Điều kiện xác định của \(P\) là:
\(\left(x+1\right)\left(2x-6\right)\ne0\Leftrightarrow\left\{{}\begin{matrix}x+1\ne0\\2x-6\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-1\\x\ne3\end{matrix}\right.\)
b) \(P=\dfrac{3x^2+3x}{\left(x+1\right)\left(2x-6\right)}\) (\(x\ne-1,x\ne3\))
\(=\dfrac{3x\left(x+1\right)}{2\left(x+1\right)\left(x-3\right)}=\dfrac{3x}{2\left(x-3\right)}\)
\(P=1\Rightarrow\dfrac{3x}{2\left(x-3\right)}=1\Rightarrow3x=2\left(x-3\right)\Leftrightarrow x=-6\) (thỏa mãn)
c) \(P>0\Rightarrow\dfrac{3x}{2\left(x-3\right)}>0\Leftrightarrow\dfrac{x}{x-3}>0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>0\\x-3>0\end{matrix}\right.\\\left[{}\begin{matrix}x< 0\\x-3< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>3\\x< 0\end{matrix}\right.\)
Kết hợp với điều kiện xác định ta được để \(P>0\) thì \(x>3\) hoặc \(x< 0,x\ne-1\).
Đúng 1
Bình luận (0)

















