Điều kiện cần và đủ để hệ phương trình m x - 4 y = m + 1 2 x + ( m + 6 ) y = m + 3 có nghiệm là
9. có nghiệm là
A. m ≠ - 4
B. m ≠ 4
C. m ≠ - 2
D. m ≠ 2
Những câu hỏi liên quan
Để hệ phương trình
x
+
y
S
x
.
y
P
có nghiệm, điều kiện cần và đủ là: A.
S
2
−
P
0
...
Đọc tiếp
Để hệ phương trình x + y = S x . y = P có nghiệm, điều kiện cần và đủ là:
A. S 2 − P < 0
B. S 2 − P ≥ 0
C. S 2 − 4 P < 0
D. S 2 − P ≥ 0
- Ta có: x, y là nghiệm phương trình X 2 - S X + P = 0
- Hệ phương trình có nghiệm khi ∆ = S 2 - 4 P ≥ 0
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Để hệ phương trình
x
+
y
S
x
y
P
có nghiệm, điều kiện cần và đủ là: A.
S
2
–
P
0
B. ...
Đọc tiếp
Để hệ phương trình x + y = S x y = P có nghiệm, điều kiện cần và đủ là:
A. S 2 – P < 0
B. S 2 – P ≥ 0
C. S 2 – 4 P < 0
D. S 2 – 4 P ≥ 0
Để hệ phương trình
x
+
y
S
x
.
y
P
có nghiệm, điều kiện cần và đủ là: A.
S
2
- P 0 B.
S
2
- P
≥
0 C. ...
Đọc tiếp
Để hệ phương trình x + y = S x . y = P có nghiệm, điều kiện cần và đủ là:
A. S 2 - P < 0
B. S 2 - P ≥ 0
C. S 2 - 4P < 0
D. S 2 - 4P ≥ 0
Đáp án D
Hệ phương trình đối xứng loại 1 với cách đặt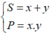 
điều kiện
S
2
≥
4
P
⇔
S
2
-
4
P
≥
0
Đúng 0
Bình luận (0)
Cho hệ phương trình
x
+
2
y
2
m
x
−
y
m
. Trong trường hợp hệ phương trình có nghiệm duy nhất (x; y), tìm điều kiện của m để x 1 và y...
Đọc tiếp
Cho hệ phương trình x + 2 y = 2 m x − y = m . Trong trường hợp hệ phương trình có nghiệm duy nhất (x; y), tìm điều kiện của m để x > 1 và y > 0
A. m > 0
B. m > 1
C. m < −1
D. m > 2
Ta có x + 2 y = 2 m x − y = m
⇔ x = 2 − 2 y m 2 − 2 y − y = m ⇔ x = 2 − 2 y 2 m + 1 y = m
Để phương trình có nghiệm duy nhất thì m ≠ - 1 2
Suy ra y = m 2 m + 1 ⇒ x = 2 − 2. m 2 m + 1 ⇒ x = 2 m + 2 2 m + 1
Vậy hệ có nghiệm duy nhất x = 2 m + 2 2 m + 1 y = m 2 m + 1
Để x > 1 y > 0
⇔ 2 m + 2 2 m + 1 > 1 m 2 m + 1 > 0 ⇔ 1 2 m + 1 > 0 m 2 m + 1 > 0 ⇔ 2 m + 1 > 0 m > 0 ⇔ m > − 1 2 m > 0 ⇒ m > 0
Kết hợp điều kiện m ≠ - 1 2 ta có m > 0
Đáp án: A
Đúng 1
Bình luận (0)
Cho hàm số yf(x). Đồ thị hàm số yf’(x) như hình vẽCho bất phương trình
3
.
f
x
≥
x
3
-
3
x
+
m
, (m là tham số thực). Điều kiện cần và đủ để bất phương trình
3
.
f
x
≥
x
3
-
3
x
+
m
đúng với mọi x thuộc đoạn
-...
Đọc tiếp
Cho hàm số y=f(x). Đồ thị hàm số y=f’(x) như hình vẽ
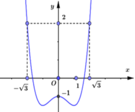
Cho bất phương trình 3 . f x ≥ x 3 - 3 x + m , (m là tham số thực). Điều kiện cần và đủ để bất phương trình 3 . f x ≥ x 3 - 3 x + m đúng với mọi x thuộc đoạn - 3 ; 3 là
A. m ≥ 3 f - 3
B. m ≤ 3 f 3
C. m ≥ 3 f 1
D. m ≤ 3 f 0
Cho hệ phương trình: (2m-1)x+y=5 và 3x-y=m . Tìm điều kiện của m để hệ phương trình có nghiệm duy nhất
Cho hàm số yf(x) có đạo hàm liên tục trên , đồ thị hàm số yf’(x) như hình vẽ bên dưới. Cho bất phương trình
f
e
x
+
2
3
e
3
x
-
e
x
-
m
≥
0
; với m là tham số thực. Tìm điều kiện cần và đủ để bất phương trình
f
e...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên , đồ thị hàm số y=f’(x) như hình vẽ bên dưới. Cho bất phương trình f e x + 2 3 e 3 x - e x - m ≥ 0 ; với m là tham số thực. Tìm điều kiện cần và đủ để bất phương trình f e x + 2 3 e 3 x - e x - m ≥ 0 đúng với mọi x ∈ - 2 ; 2
A. m ≤ f e + 2 3 e 3 - e
B. m ≤ f 1 - 1 3
C. m ≤ f 1 e + 2 3 e - 3 - e - 1
D. m ≤ f e 2 + 2 3 e 3 2 - e 2
Cho hệ phương trình: Căn 1+x + Căn 6-y = m căn 14 Và Căn 6-x + Căn 1+y = m Căn 14 Với m là tham số Tìm điều kiện của tham số m để hệ phương trình có nghiệm duy nhất
Xem chi tiết
Em nên chèn bằng công thức nhé, chứ em viết thế này cô không hiểu đúng đề bài em cần được để trợ giúp em đâu
Đúng 1
Bình luận (0)
Cho hàm số yf(x). Đồ thị hàm số yf(x) như hình vẽ. Đặt
g
(
x
)
3
f
(
x
)
-
x
3
+
3
x
-
m
, với m là tham số thực. Điều kiện cần và đủ để bất phương trình
g
x
≥
0
nghiệm đúng với
x
∈
-
3
;
3...
Đọc tiếp
Cho hàm số y=f(x). Đồ thị hàm số y=f'(x) như hình vẽ. Đặt g ( x ) = 3 f ( x ) - x 3 + 3 x - m , với m là tham số thực. Điều kiện cần và đủ để bất phương trình g x ≥ 0 nghiệm đúng với x ∈ - 3 ; 3 là
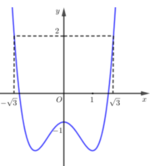
A. m ≤ 3 f 3
B. m ≤ 3 f 0
C. m ≥ 3 f 1
D. m ≥ 3 f - 3
