1: \(-1< =cosx< =1\)

=>\(-3< =3\cdot cosx< =3\)

=>\(y\in\left[-3;3\right]\)

2:

TXĐ là D=R

3: \(L=\lim\limits\dfrac{-3n^3+n^2}{2n^3+5n-2}\)

\(=\lim\limits\dfrac{-3+\dfrac{1}{n}}{2+\dfrac{5}{n^2}-\dfrac{2}{n^3}}=-\dfrac{3}{2}\)

4:

\(L=lim\left(3n^2+5n-3\right)\)

\(=\lim\limits\left[n^2\left(3+\dfrac{5}{n}-\dfrac{3}{n^2}\right)\right]\)

\(=+\infty\) vì \(\left\{{}\begin{matrix}lim\left(n^2\right)=+\infty\\\lim\limits\left(3+\dfrac{5}{n}-\dfrac{3}{n^2}\right)=3>0\end{matrix}\right.\)

5:

\(\lim\limits_{n\rightarrow+\infty}n^3-2n^2+3n-4\)

\(=\lim\limits_{n\rightarrow+\infty}n^3\left(1-\dfrac{2}{n}+\dfrac{3}{n^2}-\dfrac{4}{n^3}\right)\)

\(=+\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{n\rightarrow+\infty}n^3=+\infty\\\lim\limits_{n\rightarrow+\infty}1-\dfrac{2}{n}+\dfrac{3}{n^2}-\dfrac{4}{n^3}=1>0\end{matrix}\right.\)

\(1,y=3cosx\)

\(+TXD\) \(D=R\)

Có \(-1\le cosx\le1\)

\(\Leftrightarrow-3\le3cosx\le3\)

Vậy có tập giá trị \(T=\left[-3;3\right]\)

\(2,y=cosx\)

\(TXD\) \(D=R\)

\(3,L=lim\dfrac{n^2-3n^3}{2n^3+5n-2}=lim\dfrac{\dfrac{1}{n}-3}{2+\dfrac{5}{n^2}-\dfrac{2}{n^3}}\)(chia cả tử và mẫu cho \(n^3\))

\(=\dfrac{lim\dfrac{1}{n}-lim3}{lim2+5lim\dfrac{1}{n^2}-2lim\dfrac{1}{n^3}}=\dfrac{0-3}{2+5.0-2.0}=-\dfrac{3}{2}\)

\(4,L=lim\left(3n^2+5n-3\right)\\ =lim\left(3+\dfrac{5}{n}-\dfrac{3}{n^2}\right)\\ =lim3+5lim\dfrac{1}{n}-3lim\dfrac{1}{n^2}\\ =3\)

\(5,\lim\limits_{n\rightarrow+\infty}\left(n^3-2n^2+3n-4\right)\\ =lim\left(1-\dfrac{2}{n}+\dfrac{3}{n^2}-\dfrac{4}{n^3}\right)\\ =lim1-0\\ =1\)

Chọn B.

Ta có: 

- Ta có : 1 + 3 + 5 + ... + (2n + 1) là tổng của cấp số cộng có n số hạng với u1 = 1 và công sai d = 2

- Do đó:

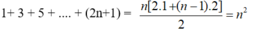
- Suy ra:

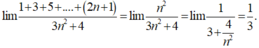
Chọn B

- Ta có : 1 + 3 + 5 + ... + (2n + 1) là tổng n số hạng của 1 cấp số cộng với số hạng đầu u 1   =   1  và công sai d = 2

- Do đó:

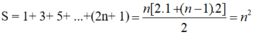
- Suy ra:

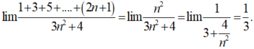
Chọn B.

3:

\(\lim\limits_{n\rightarrow\infty}\dfrac{2-5^{n-2}}{3^n+2\cdot5^n}\)

\(=\lim\limits_{n\rightarrow\infty}\dfrac{\dfrac{2}{5^n}-\dfrac{5^{n-2}}{5^n}}{\dfrac{3^n}{5^n}+2\cdot\dfrac{5^n}{5^n}}\)

\(=\lim\limits_{n\rightarrow\infty}\dfrac{\dfrac{2}{5^n}-\dfrac{1}{25}}{\left(\dfrac{3}{5}\right)^n+2\cdot1}\)

\(=-\dfrac{1}{25}:2=-\dfrac{1}{50}\)

1:

\(=\lim\limits_{n\rightarrow\infty}\dfrac{3^n-4^n\cdot4}{3^n\cdot9+4^n}\)

\(=\lim\limits_{n\rightarrow\infty}\dfrac{\dfrac{3^n}{4^n}-4}{3^n\cdot\dfrac{9}{4^n}+1}\)

\(=-\dfrac{4}{1}=-4\)

\(\lim\limits_{x\rightarrow5}\dfrac{\sqrt{x-1}-2}{\sqrt{x+4}-3}=\lim\limits_{x\rightarrow5}\dfrac{\left(\sqrt{x-1}-2\right)\left(\sqrt{x-1}+2\right)\left(\sqrt{x+4}+3\right)}{\left(\sqrt{x+4}-3\right)\left(\sqrt{x+4}+3\right)\left(\sqrt{x+1}+2\right)}\)

\(=\lim\limits_{x\rightarrow5}\dfrac{\left(x-5\right)\left(\sqrt{x+4}+3\right)}{\left(x-5\right)\left(\sqrt{x+1}+2\right)}=\lim\limits_{x\rightarrow5}\dfrac{\sqrt{x+4}+3}{\sqrt{x+1}+2}=\dfrac{3+3}{2+2}=\dfrac{3}{2}\)

\(\lim\limits\dfrac{3^{2n}+5}{4^{n+2}-9^{n-1}}=\lim\dfrac{9^n+5}{16.4^n-\dfrac{1}{9}.9^n}=\lim\dfrac{1+5.\left(\dfrac{1}{9}\right)^n}{16.\left(\dfrac{4}{9}\right)^n-\dfrac{1}{9}}\)

\(=\dfrac{1+5.0}{16.0-\dfrac{1}{9}}=-9\)

Ta có : (...) = \(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{5-x^3}-\left(x+1\right)-\left[\sqrt[3]{x^2+7}-\left(x+1\right)\right]}{x^2-1}\)

\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{5-x^3}-\left(x+1\right)}{x^2-1}=\lim\limits_{x\rightarrow1}\dfrac{5-x^3-\left(x+1\right)^2}{\left(\sqrt{5-x^3}+x+1\right)\left(x^2-1\right)}\)  

\(=\lim\limits_{x\rightarrow1}\dfrac{-x^3-x^2-2x+4}{...}\)  \(=\lim\limits_{x\rightarrow1}\dfrac{-\left(x^2+2x+4\right)\left(x-1\right)}{...}\)   

= \(\lim\limits_{x\rightarrow1}\dfrac{-\left(x^2+2x+4\right)}{\left(x+1\right)\left(\sqrt{5-x^3}+x+1\right)}=\dfrac{-7}{8}\)

\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x^2+7}-\left(x+1\right)}{x^2-1}=\lim\limits_{x\rightarrow1}\dfrac{x^2+7-x^3-3x^2-3x-1}{\left(x^2-1\right)\left[\sqrt[3]{\left(x+7\right)^2}+\left(x+1\right)\sqrt[3]{x^2+7}+\left(x+1\right)^2\right]}\)

\(=\lim\limits_{x\rightarrow1}\dfrac{-\left(x^2+3x+6\right)\left(x-1\right)}{...}\)  

\(=\lim\limits_{x\rightarrow1}\dfrac{-\left(x^2+3x+6\right)}{\left(x+1\right)\left[\sqrt[3]{\left(x^2+7\right)^2}+\sqrt[3]{x^2+7}\left(x+1\right)+\left(x+1\right)^2\right]}\)

\(=\dfrac{-\left(1+3+6\right)}{\left(1+1\right)\left(4+2.2+4\right)}=\dfrac{-5}{12}\)

Suy ra : \(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{5-x^3}-\sqrt[3]{x^2+7}}{x^2-1}=\dfrac{-7}{8}+\dfrac{5}{12}=\dfrac{-11}{24}\)

Cách 2 : Tách : \(\sqrt{5-x^3}-2-\left(\sqrt[3]{x^2+7}-2\right)\) -> Dùng liên hợp