Một cấp số nhân có hai số hạng liên tiếp là 16 và 36. Số hạng tiếp theo là:
A. 720
B. 81.
C. 64
D. 56.
Tìm a, b biết rằng: 1, a, b là 3 số hạng liên tiếp của cấp số cộng và 1 ; a 2 ; b 2 là 3 số hạng liên tiếp của một cấp số nhân.
A.a=1;b=1
B. a=-1;b=-3
C.a=1;b=3
D.Tất cả sai
Ba số có tổng là 217 có thể coi là các số hạng liên tiếp của một cấp số nhân, hoặc là các số hạng thứ hai, thứ 9 và thứ 44 của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng đầu của cấp số cộng để tổng của chúng là 820 ?
Gọi ba số đó là \(x,y,z\). Do ba số là các số hạng thứ hai, thứ 9 và thứ 44 của một cấp số cộng nên:
\(x;y=x+7d;z=x+42d\). (Với d là công sai của cấp số cộng).
Ta có: \(x+y+z=x+x+7d+x+42d=3x+49d=217\).
Mặt khác x, y, z là các số hạng liên tiếp của một cấp số nhân nên:
\(y^2=xz\)\(\Leftrightarrow\left(x+7d\right)^2=x\left(x+42d\right)\)\(\Leftrightarrow-28xd+49d^2=0\)\(\Leftrightarrow7d\left(-4x+7d\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}d=0\\-4x+7d=0\end{matrix}\right.\).
Với \(d=0\) suy ra \(x=y=z=\dfrac{217}{3}\).
Suy ra: \(n=820:\dfrac{217}{3}=\dfrac{2460}{217}\notin N\).
Với \(4+7d=0\). Ta có hệ:
\(\left\{{}\begin{matrix}4x+7d=0\\3x+49d=217\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=7\\d=4\end{matrix}\right.\).
Vậy \(u_1=7-4=3\).
Có \(S_n=\dfrac{\left[2u_1+\left(n-1\right)d\right]n}{2}=\dfrac{\left[2.3+\left(n-1\right)4\right]n}{2}=820\)
\(\Rightarrow n=20\left(tm\right)\).
Ba số phân biệt có tổng 217, là các số hạng liên tiếp của một cấp số nhân, theo thứ tự đó chúng lần lượt là số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Biết tổng của n số hạng đầu tiên của cấp số cộng là 820, khi đó n bằng
A. 21
B. 42
C. 20
D. 17
Chọn C
Gọi ba số đó lần lượt là x,y,z
Do ba số là các số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng nên ta có liên hệ: y = x + 7 d , z = x + 42 (với d là công sai của cấp số cộng)
Theo giả thiết ta có: x + y + z = x + x + 7 d + x + 42 d = 3 x + 49 d = 217
Mặt khác do x,y,z là các số hạng liên tiếp của một cấp số nhân nên
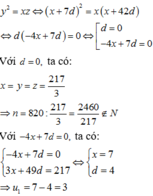
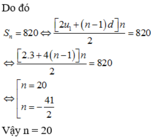
Ba số phân biệt có tổng 217, là các số hạng liên tiếp của một cấp số nhân, theo thứ tự đó chúng lần lượt là số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Biết tổng của n số hạng đầu tiên của cấp số cộng là 820, khi đó n bằng
A. 21
B. 42
C.20
D. 17
Có một dãy số với hai số hạng đầu tiên là 64 và 36 , mỗi số hạng tiếp theo là trung bình cộng của tất cả các số hạng trước đó , hãy tìm tổng của 2020 số hạng đầu tiên
Số hạng thứ 3 là: (64 + 36) : 2 = 50
Số hạng thứ 4 là: (64 + 36 + 50) : 3 = 50
Vì là trung bình cộng nên các số sau khi cộng vào rồi chia vẫn sẽ được số hạng thứ 3 (50)
=> Tổng của 2020 số hạng đầu tiên là:
64 + 36 + 50 . 2018 = 101000
Đáp số: 101000
#Shinobu Cừu
Tổng 2 số hạng đầu là: 64 + 56 = 100 = 2 x 50
Số hạng thứ 3 là: 2 x 50 : 2 = 50
Số hạng thứ 4 là: ( 2 x 50 + 50 ) : 3 = ( 3 x 50 ) : 3 = 50
Số hạng thứ 5 là: ( 4 x 50 ) : 4 = 50
Số hạng thứ 6 là: ( 5 x 50) : 5 = 50
.....
Số hạng thứ 2020 là: ( 2019 x 50 ) : 2019 = 50
Tổng của 2020 số hạng đầu tiên là: 2020 x 50 = 101 000
Đáp số:...
Ba số khác nhau có tổng bằng 114 có thể coi là ba số hạng liên tiếp của một cấp số nhân, hoặc coi là số hạng thứ nhất, thứ tư và thứ hai mươi lăm của một cấp số cộng. Tìm các số đó ?
Gọi 3 số đó là: \(a,b,c\). Theo bài ra ta có:\(\left\{{}\begin{matrix}a+b+c=114\\b^2=ac\end{matrix}\right.\). (*)
Mặt khác nó lần lượt là số hạng thứ nhất, thứ tư và thứ hai mươi lăm của một cấp số cộng nên: \(a=u_1;b=u_1+3d;c=u_1+24d\). ( với \(u_1\) là số hạng đầu của cấp số cộng, d là công sai).
Thay vào (*) ta có:
\(\left\{{}\begin{matrix}u_1+u_1+3d+u_1+24d=114\\\left(u_1+3d\right)^2=u_1\left(u_1+24d\right)\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1+9d=38\\18u_1d-9d^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+9d=38\\9d\left(2u_1-d\right)=0\end{matrix}\right.\).
Nếu \(d=0\) thì a,b,c là ba số hạng của một cấp số cộng không đổi nên \(a=b=c=\sqrt[3]{114}\).
Nếu \(d\ne0\) suy ra: \(\left\{{}\begin{matrix}u_1+9d=38\\2u_1-d=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u_1=2\\d=4\end{matrix}\right.\).
Khi đó \(a=2;b=2+3.4=16;c=2+24.3=74\).
Câu 1:
Cho một dãy số có các số hạng đầu tiên là 1,8,22,43,..... Hiệu của 2 số hạng liên tiếp của dãy đó lập thành một cấp số cộng: 7,14,21,...7n. Số 35351 là số hạng thứ mấy của cấp số đã cho?
Câu 2:
Cho tam giác ABC, có 3 cạnh a,b,c theo thứ tự lập thành 1 cấp số cộng. Tính giá trị biểu thức P= cot\(\dfrac{A}{2}\). cot \(\dfrac{C}{2}\)
Câu 3:
Cho 2 cấp số cộng hữu hạn, mỗi cấp số có 100 số hạng:4,7,10,13,16,... và 1,6,11,16,21,... Hỏi có tất cả bao nhiêu số có mặt trong cả 2 cấp số trên?
Câu 1:
Dãy đã cho có thể viết dưới dạng công thức truy hồi sau:
\(\left\{{}\begin{matrix}u_1=1\\u_{n+1}=u_n+7n\end{matrix}\right.\)
\(u_{n+1}=u_n+7n\Leftrightarrow u_{n+1}-\dfrac{7}{2}\left(n+1\right)^2+\dfrac{7}{2}\left(n+1\right)=u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n\)
Đặt \(v_n=u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n\Rightarrow\left\{{}\begin{matrix}v_1=1\\v_{n+1}=v_n\end{matrix}\right.\)
\(\Rightarrow v_{n+1}=v_n=v_{n-1}=...=v_1=1\)
\(\Rightarrow u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n=1\)
\(\Leftrightarrow u_n=\dfrac{7}{2}n^2-\dfrac{7}{2}n+1\)
\(\dfrac{7}{2}n^2-\dfrac{7}{2}n+1=35351\)
\(\Leftrightarrow\dfrac{7}{2}n^2-\dfrac{7}{2}n-35350=0\)
\(\Rightarrow n=101\)
Vậy đó là số hạng thứ 101
2.
Do a;b;c lập thành 1 cấp số cộng
\(\Rightarrow a+c=2b\)
\(\Leftrightarrow2R.sinA+2R.sinC=2.2R.sinB\)
\(\Leftrightarrow sinA+sinC=2sinB\)
\(\Leftrightarrow2sin\dfrac{A+C}{2}.cos\dfrac{A-C}{2}=4sin\dfrac{B}{2}cos\dfrac{B}{2}\)
\(\Leftrightarrow cos\dfrac{B}{2}cos\dfrac{A-C}{2}=2sin\dfrac{B}{2}cos\dfrac{B}{2}\)
\(\Leftrightarrow cos\dfrac{A-C}{2}=2sin\dfrac{B}{2}=2cos\dfrac{A+C}{2}\)
\(\Leftrightarrow cos\left(\dfrac{A}{2}\right)cos\left(\dfrac{C}{2}\right)+sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)=2cos\left(\dfrac{A}{2}\right)cos\left(\dfrac{C}{2}\right)-2sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)\)
\(\Leftrightarrow cos\left(\dfrac{A}{2}\right).cos\left(\dfrac{C}{2}\right)=3sin\left(\dfrac{A}{2}\right).sin\left(\dfrac{C}{2}\right)\)
\(\Leftrightarrow cot\left(\dfrac{A}{2}\right).cot\left(\dfrac{C}{2}\right)=3\)
3.
Công thức số hạng tổng quát của dãy đầu: \(u_n=4+3\left(n-1\right)=3n+1\)
Với \(1\le n\le100\)
Công thức số hạng tổng quát của dãy sau: \(v_m=1+5\left(m-1\right)=5m-4\)
Với \(1\le m\le100\)
Các số hạng của 2 dãy trùng nhau khi:
\(3n+1=5m-4\)
\(\Leftrightarrow5m=3n+5\Leftrightarrow m=\dfrac{3n}{5}+1\)
\(\Rightarrow n⋮5\Rightarrow n=5k\)
Mà \(1\le n\le100\Rightarrow1\le5k\le100\Rightarrow1\le k\le20\)
\(\Rightarrow\) Hai dãy số có 20 số hạng trùng nhau
Vậy số số có mặt trong 2 dãy trên là: \(100+100-20=180\) số
Ba số có tổng là 217 có thể coi là các số hạng liên tiếp của một cấp số nhân, hoặc là các số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng. Hỏi phải lấy bao nhiêu số hạng đầu của cấp số cộng để tổng của chúng là 820?
Tìm 3 số hạng liên tiếp a,b,c của 1 cấp số nhân biết a+b+c=14và abc=64