7. Cho bảng "tần số"

Từ bảng trên hãy viết lại một bảng số liệu ban đầu
A. 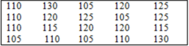
B. 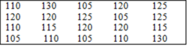
C. 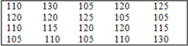
D. 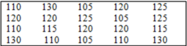
Cho bảng "tần số"

Từ bảng trên hãy viết lại một bảng số liệu ban đầu
A. 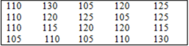
B. 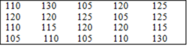
C. 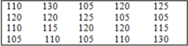
D. 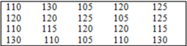
Ta có thể lập một bảng như sau: (ví dụ đem kiểm tra số lượng dầu trong một số thùng dầu trong kho
Đáp án cần chọn là: B
Cho bảng “tần số”:
| Giá trị (x) | 110 | 115 | 120 | 125 | 130 | |
| Tần số (n) | 4 | 7 | 9 | 8 | 2 | N = 30 |
Hãy từ bảng này viết lại một bảng số liệu ban đầu.
| 110 | 120 | 125 | 110 | 115 | 120 |
| 115 | 110 | 120 | 115 | 120 | 125 |
| 125 | 115 | 120 | 120 | 125 | 125 |
| 125 | 125 | 110 | 120 | 120 | 115 |
| 130 | 115 | 115 | 125 | 130 | 120 |
Cho bảng tần số
Cho bảng tần số
Giá trị (x) 105 110 115 120 125 130
Tần số (n) 8 4 6 6 4 2 N= 30
Hãy từ bảng này viết lại một bảng số liệu ban đầu
105 105 105 105 105 105 105 105 110 110 110 110
115 115 115 115 115 115 120 120 120 120 120 120
125 125 125 125 130 130
Ko kẻ bảng đc! Sorry nha!
Chúc bạn học tốt!![]()
1.Cho bảng tần số
Giá trị (x) 110 115 120 125 130
Tần số (n) 4 7 9 8 2 N=30
HÃy từ bảng này viết lại bảng số liệu ban đầu
Cho bảng tần số :
Gía trị(x) 110 115 120 125 130
Tần số(n) 4 7 9 8 2 N=30
a.Hãy từ bảng này viết lại 1 bảng số liệu ban đầu.
b.Tìm số trung bình cộng.
c.Tìm mốt .
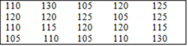
Một giáo viên dạy Giáo dục thể chất đã thống kê thời gian chạy 100 m (tính theo giây) của 20 học sinh nam và ghi lại trong bảng số liệu ban đầu như sau:

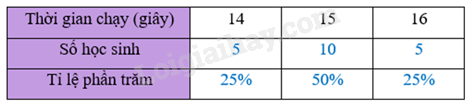
a) Chuyển dữ liệu từ bảng số liệu ban đầu ở trên sang dạng bảng thống kê sau đây:

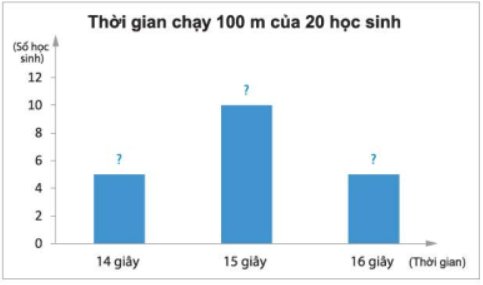
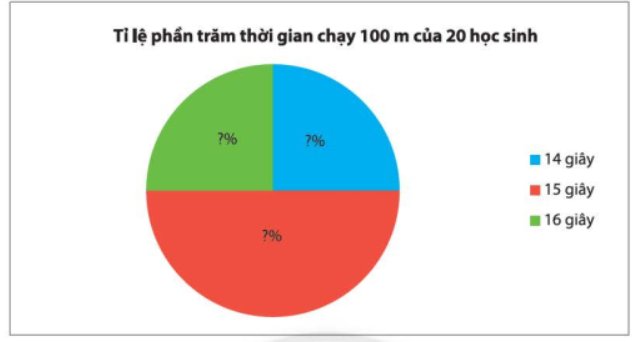
b) Hãy chuyển dữ liệu từ bảng thống kê ở câu a sang dạng biểu đồ cột và biểu đồ hình quạt tròn sau đây:
Biểu đồ cột:
Biểu đồ hình quạt tròn:
a) Chuyển dữ liệu từ bảng số liệu ban đầu ở trên sang dạng bảng thống kê sau đây:
b) Biểu đồ cột biểu diễn thời gian chạy 100 m (tính theo giây) của 20 học sinh nam:
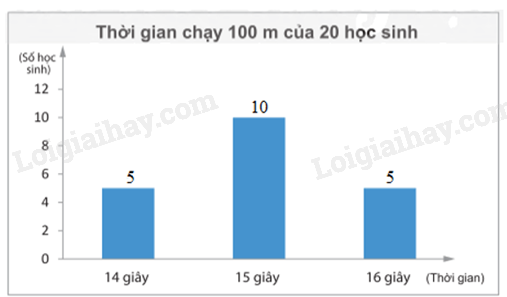
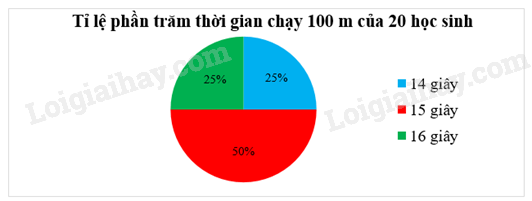
Biểu đồ hình quạt tròn biểu diễn thời gian chạy 100 m (tính theo giây) của 20 học sinh nam:
Số điểm một cầu thủ bóng rổ ghi được trong 20 trận đấu được cho ở bảng sau:

a) Tìm tứ phân vị của dãy số liệu trên.
b) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:
c) Hãy ước lượng tứ phân vị của số liệu từ bảng tần số ghép nhóm trên.
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:

Tứ phân vị thứ nhất là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right) = \frac{1}{2}\left( {11 + 11} \right) = 11\)
Tứ phân vị thứ hai là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right) = \frac{1}{2}\left( {14 + 14} \right) = 14\)
Tứ phân vị thứ ba là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right) = \frac{1}{2}\left( {21 + 22} \right) = 21,5\)
b)

c) Do số trận đấu là số nguyên nên ta hiệu chỉnh như sau:

Tổng trận đấu là: \(n = 4 + 8 + 2 + 6 = 20\).
Gọi \({x_1};{x_2};...;{x_{20}}\) là điểm số của các trận đấu được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_4} \in \begin{array}{*{20}{c}}{\left[ {5,5;10,5} \right)}\end{array};{x_5},...,{x_{12}} \in \begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array};{x_{13}},{x_{14}} \in \begin{array}{*{20}{c}}{\left[ {15,5;20,5} \right)}\end{array};{x_{15}},...,{x_{20}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right)\)
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_{10}},{x_{11}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{2} - 4}}{8}.\left( {15,5 - 10,5} \right) = 14,25\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right)\).
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_5},{x_6} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{4} - 4}}{8}.\left( {15,5 - 10,5} \right) = 11,125\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\).
Ta có: \(n = 20;{n_j} = 6;C = 4 + 8 + 2 = 14;{u_j} = 20,5;{u_{j + 1}} = 25,5\)
Do \({x_{15}},{x_{16}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 20,5 + \frac{{\frac{{3.20}}{4} - 14}}{6}.\left( {25,5 - 20,5} \right) \approx 21,3\)
Cho bảng"tần số"
| Giá trị(x) | 110 | 115 | 120 | 125 | 130 | |
| Tần số(n) | 4 | 7 | 9 | 8 | 2 | N=30 |
Hãy từ bảng này viết lại bảng số liệu ban đầu
cho bảng tần số
| gia trị (x) | 110 | 115 | 120 | 125 | 180 | |
| tần số ( n ) | 4 | 7 | 9 | 8 | 2 | N=30 |
từ bảng trên hãy viết lại bảng số liệu ban đầu