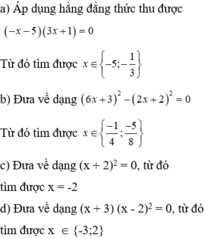Giải các phương trình sau: | 4x | = 2x + 12

Những câu hỏi liên quan
Giải các phương trình sau: | 4x | = 2x + 12
Ta có: | 4x | = 2x + 12
+ Với x ≥ 0, phương trình tương đương: 4x = 2x + 12 ⇔ 2x = 12 ⇔ x = 6
Thỏa mãn điều kiện x ≥ 0
+ Với x < 0, phương trình tương đương: - 4x = 2x + 12 ⇔ - 6x = 12 ⇔ x = - 2
Thỏa mãn điều kiện x < 0
Vậy phương trình đã cho có tập nghiệm là S = { - 2;6 }
Đúng 0
Bình luận (0)
1) Giải các phương trình sau : a) x-3/x=2-x-3/x+3 b) 3x^2-2x-16=0 2) Giải bất phương trình sau: 4x-3/4>3x-5/3-2x-7/12
\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
Đúng 1
Bình luận (0)
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)
Đúng 1
Bình luận (0)
Giải các phương trình sau: 1)√3x²-√12=0
2)√(x-3)²=9
3)√4x²+4x+1=6
4)√(2x-1)²=3
5)√(x-3)²=3-x 6)√4x²-20x+25+2x=5
7)√1-12x+36x²=5
1.
$\sqrt{3x^2}-\sqrt{12}=0$
$\Leftrightarrow \sqrt{3x^2}=\sqrt{12}$
$\Leftrightarrow 3x^2=12$
$\Leftrightarrow x^2=4$
$\Leftrightarrow (x-2)(x+2)=0\Leftrightarrow x=\pm 2$
Đúng 0
Bình luận (0)
2.
$\sqrt{(x-3)^2}=9$
$\Leftrightarrow |x-3|=9$
$\Leftrightarrow x-3=9$ hoặc $x-3=-9$
$\Leftrightarrow x=12$ hoặc $x=-6$
Đúng 0
Bình luận (0)
3.
$\sqrt{4x^2+4x+1}=6$
$\Leftrightarrow \sqrt{(2x+1)^2}=6$
$\Leftrightarrow |2x+1|=6$
$\Leftrightarrow 2x+1=6$ hoặc $2x+1=-6$
$\Leftrightarrow x=\frac{5}{2}$ hoặc $x=\frac{-7}{2}$
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
giải các phương trình sau
a) x2+4x-5=0
b) x2-x-12=0
c) (2x-7)2-6(2x-7)(x-3)=0
`a,x^2 +4x-5=0`
`<=> x^2-x+5x-5=0`
`<=> x(x-1)+5(x-1)=0`
`<=>(x-1)(x+5)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-5\end{matrix}\right.\)
`b, x^2 -x-12=0`
`<=> x^2 +3x-4x-12=0`
`<=>(x^2+3x)-(4x+12)=0`
`<=>x(x+3)-4(x+3)=0`
`<=>(x+3)(x-4)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=4\end{matrix}\right.\)
`c, (2x-7)^2 - 6(2x-7)(x-3)=0`
`<=>(2x-7)(2x-7 -6x+18)=0`
`<=>(2x-7) ( -4x+11)=0`
\(\Leftrightarrow\left[{}\begin{matrix}2x-7=0\\-4x+11=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=7\\-4x=-11\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=\dfrac{11}{4}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
a: =>(x+5)(x-1)=0
=>x=1 hoặc x=-5
b: =>(x-4)(x+3)=0
=>x=4 hoặc x=-3
c: =>(2x-7)(2x-7-6x+18)=0
=>(2x-7)(-4x+11)=0
=>x=11/4 hoặc x=7/2
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
x
−
2
2
−
2
x
+
3
2
0
;b)
9
2
x
+
1
2
−
4...
Đọc tiếp
Giải các phương trình sau:
a) x − 2 2 − 2 x + 3 2 = 0 ;
b) 9 2 x + 1 2 − 4 x + 1 2 = 0 ;
c) x + 1 2 + 2 x + 1 + 1 = 0 ;
d) x − 1 x 2 − 9 + x + 3 = 0 .
Bài 1: Giải các bất phương trình và phương trình sau :
a) 2(3-4x) = 10-(2x – 5)
Giải các bất phương trình và phương trình sau :
a) 3(2-4x) = 11-(3x – 1)
Bài 1:
a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)
\(\Leftrightarrow6-8x-10+2x-5=0\)
\(\Leftrightarrow-6x+11=0\)
\(\Leftrightarrow-6x=-11\)
hay \(x=\dfrac{11}{6}\)
b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)
\(\Leftrightarrow6-12x-11+3x-1=0\)
\(\Leftrightarrow-9x-6=0\)
\(\Leftrightarrow-9x=6\)
hay \(x=-\dfrac{2}{3}\)
Đúng 2
Bình luận (0)
Giải các phương trình sau:a)
3
x
−
1
+
4
x
−
2
5
x
−
3
+
6
x
−
4
;
b)
2
x...
Đọc tiếp
Giải các phương trình sau:
a) 3 x − 1 + 4 x − 2 = 5 x − 3 + 6 x − 4 ;
b) 2 x − 1 2 + 2 x + 1 3 = 2 x + 7 6 + 2 x + 9 7 . Gợi ý: Thêm bớt 2.
Giải các phương trình sau:a)
7
−
x
2
4
−
x
+
5
2
0
;
b)
4
x
2
+
x
−
1...
Đọc tiếp
Giải các phương trình sau:
a) 7 − x 2 4 − x + 5 2 = 0 ;
b) 4 x 2 + x − 1 2 − 2 x + 1 2 = 0 ;
c) x 3 + 1 = x + 1 2 − x ;
d) x 2 − 4 x − 5 = 0 .
Giải các phương trình sau:a)
2
x
−
1
3
+
6
3
x
−
1
2
2
x
+
1
3
+
6...
Đọc tiếp
Giải các phương trình sau:
a) 2 x − 1 3 + 6 3 x − 1 2 = 2 x + 1 3 + 6 x + 2 3 ;
b) x − 2 2 + 3 − 2 x 2 − 4 x − 4 x − 5 = x + 3 2 ;
c) x − 3 + 2 x − 3 − 1 3 = 3 − x 4 ;
d) x + 4 3 − 1 7 = 2 − x 7 + x 3 + x + 1 .