Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h=3 là chiều cao. Biết thể tích khối nón cụt là V = π  tìm giá trị lớn nhất của biểu thức P=R+2r 

A. 2 3  

B. 3.

C. 3 3  

D. 2.

Hình bên là hình nón .chiều cao là h(cm),bán kính đường tròn đáy là r(cm) và độ dài đường sinh là m(cm) thì thể tích hình nón này là:

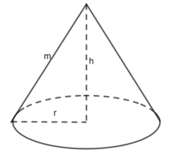
A. π . r 2 h ( c m 3 )     B. (1/3) π .  r 2 h ( c m 3 )

C. π .r.m ( c m 3 )     D. π r(r+m) ( c m 3 )

Cho khối nón có bán kính đáy r = 3 , chiều cao h = 2 . Tính thể tích V của khối nón

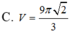
Cho khối nón có bán kính đáy r = 3, chiều cao h= 2  Tính thể tích V của khối nón.

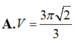
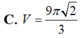
Cho khối nón có bán kính đáy r = 3 chiều cao  h = 2 . Tính thể tích V của khối nón

Cho khối nón có bán kính đáy r = 3, chiều cao h = 2  Tính thể tích V của khối nón.

A.  V = 3 π 2 3

B.  V = 3 π 2

C.  V = 9 π 2 3

D.  V = 9 π 2

Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là :

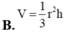
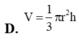
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là

A.  V = πr 2 h

B.  V = 1 3 r 2 h

C.  V = r 2 h

D.  V = 1 3 πr 2 h

Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là.