Cho số phức z = a + b i . Phương trình nào sau đây nhận z và z ¯ làm nghiệm:
A. z 2 − 2 a z + a 2 b 2 = 0
B. z 2 − 2 a z + a 2 + b 2 = 0
C. z 2 − 2 a z − a 2 − b 2 = 0
D. z 2 + 2 a z + a 2 + b 2 = 0
Những câu hỏi liên quan
Cho phương trình trên tập họp số phức
z
2
+
a
x
+
b
0
. Nếu phương trình nhận số phức
z
1
+
i
làm một nghiệm thì a và b bằng. A. a -2, b 2 B. a 1, b 5 C. a 2, b -2 D. a 2, b -4
Đọc tiếp
Cho phương trình trên tập họp số phức z 2 + a x + b = 0 . Nếu phương trình nhận số phức z = 1 + i làm một nghiệm thì a và b bằng.
A. a = -2, b = 2
B. a = 1, b = 5
C. a = 2, b = -2
D. a = 2, b = -4
Cho phương trình trên tập họp số phức
z
2
+
a
z
+
b
0
a
,
b
∈
ℝ
. Nếu phương trình nhận số phức
z
1
+
i
làm một nghiệm thì a và b bằng. A. a -2, b 2 B. a 1, b 5 C. a 2, b -2 D. a...
Đọc tiếp
Cho phương trình trên tập họp số phức z 2 + a z + b = 0 a , b ∈ ℝ . Nếu phương trình nhận số phức z = 1 + i làm một nghiệm thì a và b bằng.
A. a = -2, b = 2
B. a = 1, b = 5
C. a = 2, b = -2
D. a = 2, b = -4
Chọn A.
Phương pháp: Thế nghiệm vào phương trình và sử dụng định nghĩa về hai số phức bằng nhau.
Cách giải: Thay nghiệm z = 1+ i vào phương trình ta có:
Đúng 0
Bình luận (0)
Cho số phức
z
-
1
2
+
i
3
2
. Phương trình bậc hai với hệ số thực nhận z và
z
làm nghiệm là A.
z
2
-
z
+
2
0
B.
2
z
2
+
z
+
2
0
C. ...
Đọc tiếp
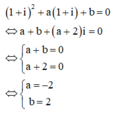
Cho số phức z = - 1 2 + i 3 2 . Phương trình bậc hai với hệ số thực nhận z và z làm nghiệm là
A. z 2 - z + 2 = 0
B. 2 z 2 + z + 2 = 0
C. z 2 - z + 1 = 0
D. z 2 + z + 1 = 0
Phương trình nào dưới đây nhận z1+
3
i và z1-√3 i làm nghiệm? A.
z
2
-
2
z
+
3
0
.
B.
z
2
-
2
z
+
4
0
.
C.
z
2
+
2
z
+
3
0...
Đọc tiếp
Phương trình nào dưới đây nhận z=1+ 3 i và z=1-√3 i làm nghiệm?
A. z 2 - 2 z + 3 = 0 .
B. z 2 - 2 z + 4 = 0 .
C. z 2 + 2 z + 3 = 0 .
D. z 2 + 2 z + 4 = 0 .
Cho z = a + bi là một số phức. Hãy tìm một phương trình bậc hai với hệ số thực nhận z và làm nghiệm
Số phức z nào dưới đây là nghiệm phương trình (1+i) z 2 - ( 2 - i ) z ¯ + i - 2 = 0 ?
A. z = 4
B. z = 1 + i
C. z = -2i
D. z = 2 - i
Cho z = a + bi là một số phức. Hãy tìm phương trình bậc hai với hệ số thực nhận z và z làm nghiệm.
Tìm các số thực a,b,c để phương trình (ẩn z)
z
3
+
a
z
2
+
b
z
+
c
0
nhận
z
1
+
i
và
z
2
làm nghiệm
Đọc tiếp
Tìm các số thực a,b,c để phương trình (ẩn z) z 3 + a z 2 + b z + c = 0 nhận z = 1 + i và z = 2 làm nghiệm
Cho số phức
z
2
−
5
i
. Tìm phương trình bậc hai nhận
1
z
và
1
z
¯
làm nghiệm. A.
29
x
2
+
4
x
+
1
0
B.
29
x
2
+...
Đọc tiếp
Cho số phức z = 2 − 5 i . Tìm phương trình bậc hai nhận 1 z và 1 z ¯ làm nghiệm.
A. 29 x 2 + 4 x + 1 = 0
B. 29 x 2 + 4 x - 1 = 0
C. 29 x 2 - 4 x + 1 = 0
D. 29 x 2 - 4 x - 1 = 0
