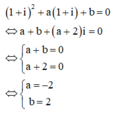
Chọn A.
Phương pháp: Thế nghiệm vào phương trình và sử dụng định nghĩa về hai số phức bằng nhau.
Cách giải: Thay nghiệm z = 1+ i vào phương trình ta có:
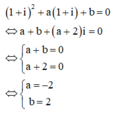
Nếu z = i là một nghiệm phức của phương trình z 2 + a z + b = 0 với a , b ∈ ℝ thì a + b bằng
A. -2
B. -1
C. 1
D. 2
Nếu z = i là nghiệm phức của phương trình z 2 + a z + b = 0 với a , b ∈ ℝ thì a + b bằng
A. -1.
B. 2.
C. -2.
D. 1.
Nếu z = i là nghiệm phức của phương trình z 2 + a z + b = 0 v ớ i a , b ∈ ℝ thì a + b bằng
A. -1
B. 2
C. -2
D. 1
Phương trình z 2 + az + b = 0 , a , b ∈ ℝ có một nghiệm phức là z = 1 + 2 i . Khi đó tổng a + b bằng
A. -4
B. 3
C. 0
D. -3
Cho số phức z = a + b i a , b ∈ ℝ thỏa mãn z + 2 + i − z 1 + i = 0 và z > 1. Tính P = a + b .
A. P = − 1.
B. P = − 5.
C. P = 3.
D. P = 7.
Nếu z = i là nghiệm phức của phương trình: z 2 + a z + b = 0 với (a,bϵR) thì a+b bằng
A. -1
B. -2
C. 1
D. 2
Cho phương trình z 3 + a z 2 + b z + c = 0 Nếu z=1-i và z=1 là 2 nghiệm của phương trình thì a - b - c bằng
A. 2
B. 3
C. 5
D. 6
Cho số phức z = a + b i a , b ∈ ℝ thỏa mãn z + 2 + i − z 1 + i = 0 , z > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Cho hai số phức z = a + bi ; a , b ∈ ℝ . Có điểm biểu diễn của số phức z nằm trong dải − 2 ; 2 (hình 1) điều kiện của a và b là: a ≥ 2 b ≥ 2 a ≤ − 2 b ≤ − 2 − 2 < a < 2 , b ∈ ℝ a , b ∈ − 2 ; 2
A. a ≥ 2 b ≥ 2
B. a ≤ − 2 b ≤ − 2
C. − 2 < a < 2 , b ∈ ℝ
D. a , b ∈ − 2 ; 2
