Đáp án C
- Nhìn vào hình vẽ ta có phần thực a bị giới hạn − 2 < a < 2 , b ∈ ℝ
Chú ý: Cho số phức z = a + bi, điểm M(a;b) trong hệ trục tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z.
Đáp án C
- Nhìn vào hình vẽ ta có phần thực a bị giới hạn − 2 < a < 2 , b ∈ ℝ
Chú ý: Cho số phức z = a + bi, điểm M(a;b) trong hệ trục tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z.
Cho số phức z = a + b i ; a , b ∈ ℝ Để điểm biểu diễn của z trên mặt phẳng tọa độ thuộc dải giới hạn bởi hai đường thẳng x = -3 và x = 3 như hình vẽ bên thì điều kiện của a và b là:
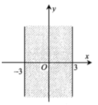
A. a ≤ - 3 b ≤ - 3
B. a ≤ 3 b ≥ - 3
C. a ≥ 3 b ≥ 3
D. - 3 ≤ a ≤ 3 b ∈ ℝ
Cho số phức z=a+bi, a,bÎR. Điểm biểu diễn của z trên mặt phẳng tọa độ thuộc dải giới hạn bởi hai đường thẳng y = -2 và y = 2 như hình vẽ bên thì điều kiện của a và b là:
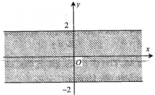
A. - 2 ≤ a ≤ 2 b ∈ R
B. a ≤ 2 b ≥ - 2
C. - 2 ≤ a ≤ 2 - 2 ≤ b ≤ 2
D. a ∈ R - 2 ≤ b ≤ 2
Cho số phức z = a + b i , a , b ∈ R . Tìm điều kiện của a và b để điểm biểu diễn của z thuộc dải giới hạn bởi đường thẳng x = - 2 và x = 2 như hình vẽ bên
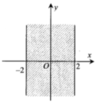
A. a ≥ 2 b ≥ 2
B. a ≤ 2 b ≤ - 2
C. a ≤ 2 b ≥ - 2
D. - 2 ≤ a ≤ 2 b ∈ R
Cho số phức z=a+bi, a,bÎR. Điểm biểu diễn z thuộc dải giới hạn bởi hai đường thẳng y = -5 và y = 5 như hình vẽ bên. Tìm điều kiện của a và b.
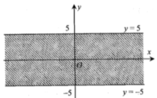
A. - 5 ≤ a ≤ 5 - 5 ≤ b ≤ 5
B. - 5 ≤ a ≤ 5 b ∈ R
C. a ∈ R - 5 ≤ b ≤ 5
D. a ≤ 5 b ≥ - 5
Trong mặt phẳng phức, gọi M là điểm biểu diễn số phức z − z ¯ 2 với z = a + b i a , b ∈ ℝ , b ≠ 0 . Chọn kết luận đúng
A. M thuộc tia Ox
B. M thuộc tia Oy
C. M thuộc tia đối của tia Ox
D. M thuộc tia đối của tia
Cho số phức z = a + b i , a , b ∈ R . Điểm biểu diễn của z trên mặt phẳng tọa độ thuộc hình tròn tâm O bán kính R = 2 như hình vẽ bên thì điều kiện của a và b là
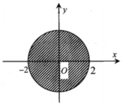
A. - 2 ≤ a ≤ 2 - 2 ≤ b ≤ 2
B. a 2 + b 2 ≤ 4
C. a 2 + b 2 > 4
D. a < - 2 ; b > 2
Cho số phức z = a + b i a , b ∈ ℝ thỏa mãn đồng thời hai điều kiện z = z ¯ - 1 - i và biểu thức A = z - 2 + 2 i + z - 3 + i đạt giá trị nhỏ nhất. Giá trị của biểu thức a+b bằng
A. -1
B. 2
C. -2
D. 1
Số phức z = a + b i a , b ∈ ℝ có z = 2 2 và z 2 có phần ảo bằng 8, điểm biểu diễn số phức z nằm trong góc phần tư thứ ba của hệ trục toạ độ. Giá trị của biểu thức P = a + b bằng
A. P = 4
B. P = 0
C. P = - 4
D. P = 2
Cho số phức z=a+bi, a,b ÎR. Tìm điều kiện của a và b để điểm biểu diễn z thuộc hình tròn tâm O bán kính R = 3 như hình vẽ bên
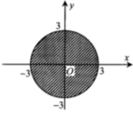
A. a 2 + b 2 > 9
B. - 3 ≤ a ≤ 3 - 3 ≤ b ≤ 3
C. a 2 + b 2 ≤ 9
D. a < - 3 b > 3