Cho các đường cong C 1 : y = x 3 - 3 x 2 + 4 , C 2 : y = - x 4 + x 2 - 3 và C 3 : y = 5 x + 2 x - 1 . Hỏi các đường cong nào có tâm đối xứng?
A. C 1 , C 2 v à C 3
B. C 1 v à C 3
C. C 2 v à C 3
D. C 1 v à C 2
Những câu hỏi liên quan
cho đường cong (C) là đồ thị của Hàm Số y = 2x^3 - 2x^2 - 4x + 1. viết phương trình tiếp tuyến của đường cong C tại điểm có hoành độ x=0
\(y'=6x^2-4x-4\)
\(y'\left(0\right)=-4\)
\(y\left(0\right)=1\)
Do đó pt tiếp tuyến tại điểm có hoành độ x=0 là:
\(y=-4\left(x-0\right)+1\Leftrightarrow y=-4x+1\)
Đúng 1
Bình luận (0)
Tính diện tích giới hạn bởi các đường cong y (x - 1)lnx và y x - 1. A.
e
2
-
4
e
+
5
4
B.
3
e
2
-
2
e
+...
Đọc tiếp
Tính diện tích giới hạn bởi các đường cong y = (x - 1)lnx và y = x - 1.
A. e 2 - 4 e + 5 4
B. 3 e 2 - 2 e + 5 2
C. 7 e 2 - e + 2 3
D. 4 e 2 + 3 e - 2 5
Chọn A.
+) Xét phương trình: (x - 1)lnx = x - 1 ⇔ x = 1 hoặc x = e.
+ ) Diện tích cần tìm là:
Đúng 0
Bình luận (0)
Tính diện tích giới hạn bởi các đường cong y(e+1)x; y (ex + 1)x A.
e
5
-
19
100
B.
2
e
3
-
73
50
C.
e
3
-
11
20
D.
e...
Đọc tiếp
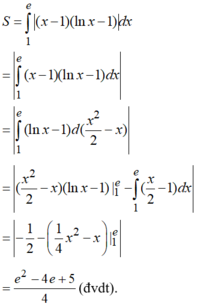
Tính diện tích giới hạn bởi các đường cong y=(e+1)x; y = (ex + 1)x
A. e 5 - 19 100
B. 2 e 3 - 73 50
C. e 3 - 11 20
D. e 2 - 1
Chọn D.
Hoành độ giao điểm của hai đường là nghiệm của phương trình (e+1)x = ( 1 + e x ) x <=> x = 0 hoặc x =1
Diện tích cần tính là S = ∫ 0 1 x e x d x - ∫ 0 1 e x d x = ∫ 0 1 x d ( e x ) - e ∫ 0 1 x d x
Đúng 0
Bình luận (0)
Cho đường cong (C) : y 3x + 1 / 1 - x Số tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng (Δ): 2x + 2y – 9 0. A. 1 B. 2 C. 3 D. 4
Đọc tiếp
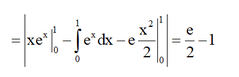
Cho đường cong (C) : y = 3x + 1 / 1 - x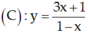 
Số tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng (Δ): 2x + 2y – 9 = 0.
A. 1
B. 2
C. 3
D. 4
Chọn A.
Tập xác định D = R \ {1}. Ta có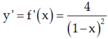 
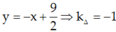
Vì tiếp tuyến vuông góc với Δ nên, 
Gọi N(xo; yo) là tọa độ tiếp điểm của tiếp tuyến, ta có f’(xo) = ktt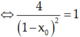 
⇔ (xo – 1)2 = 4 ⇔ xo = 3 ∨ xo = -1.
Với xo = 3 ⇒ y = -5, phương trình tiếp tuyến tại điểm này là:
⇔ y = -1(x – 3) – 5 ⇔ y = -x – 2
Với xo = -1 ⇒ y = -1, phương trình tiếp tuyến tại điểm này là:
⇔ y = -1(x + 1) – 1 ⇔ y = -x – 2.
Đúng 0
Bình luận (0)
Xét hàm số y f(x) liên tục trên miền D [a;b] có đồ thị là một đường cong C. Gọi S là phần giới hạn bởi C và các đường thẳng x a; x b Người ta chứng minh được rằng độ dài đường cong S bằng
∫
a
b
1
+
(
f
(
x
)
)
2
d
x
...
Đọc tiếp
Xét hàm số y = f(x) liên tục trên miền D = [a;b] có đồ thị là một đường cong C. Gọi S là phần giới hạn bởi C và các đường thẳng x = a; x = b Người ta chứng minh được rằng độ dài đường cong S bằng ∫ a b 1 + ( f ' ( x ) ) 2 d x Theo kết quả trên, độ dài đường cong S là phần đồ thị của hàm số f(x) = ln x và bị giới hạn bởi các đường thẳng x = 1 ; x = 3 là m - m + ln 1 + m n với m , n ∈ R thì giá trị của m 2 - m n + n 2 là bao nhiêu?
A. 6
B. 7
C. 3
D. 1
Hình phẳng giới hạn bởi các đường cong
y
x
(
1
-
x
)
và
y
x
3
-
x
có diện tích bằng
Đọc tiếp
Hình phẳng giới hạn bởi các đường cong y = x ( 1 - x ) và y = x 3 - x có diện tích bằng
Hình phẳng giới hạn bởi các đường cong
y
x
(
1
-
x
)
và
y
x
3
-
x
có diện tích bằng
A
.
37
12
B
.
5
12
C
.
8
3...
Đọc tiếp
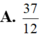
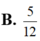
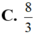
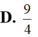
Hình phẳng giới hạn bởi các đường cong y = x ( 1 - x ) và y = x 3 - x có diện tích bằng
A . 37 12
B . 5 12
C . 8 3
D . 9 4
1)Viết phương trình tiếp tuyến của đường cong (C):yf(x)x^3-2x biết: a)tiếp tuyến vuông góc với trục Ox. b)Tại giao điểm của (C) với các trục tọa độ.2)Cho hàm số :yf(x)x-1/x có đồ thị là đường cong (C):a) Viết pt tt với (C),biết tt song song với dt y2x và tiếp điểm có hoành độ âm.b)CMR trên (C) không thể tồn tại 2 điểm M,N để tiếp tuyến tại 2 điểm này vuông góc với nhau.c)CMR mọi tiếp tuyến của (C) đều không thể đi qua gốc tọa độ O.3)Tìm tất cả các điểm trên đồ thị (C):yf(x)(2x+3)/(x+2) sao cho t...
Đọc tiếp
1)Viết phương trình tiếp tuyến của đường cong (C):y=f(x)=x^3-2x biết: a)tiếp tuyến vuông góc với trục Ox. b)Tại giao điểm của (C) với các trục tọa độ.
2)Cho hàm số :y=f(x)=x-1/x có đồ thị là đường cong (C):
a) Viết pt tt với (C),biết tt song song với dt y=2x và tiếp điểm có hoành độ âm.
b)CMR trên (C) không thể tồn tại 2 điểm M,N để tiếp tuyến tại 2 điểm này vuông góc với nhau.
c)CMR mọi tiếp tuyến của (C) đều không thể đi qua gốc tọa độ O.
3)Tìm tất cả các điểm trên đồ thị (C):y=f(x)=(2x+3)/(x+2) sao cho tại điểm đó tt của (C) cắt các đường thằng (d1):x=-2 và (d2):y=2 lần lượt tại A và B sao cho AB gần nhất.
4)Cho hàm số y=f(x)=sin2x+1 (x>=0) và =2x+1 (x<0) .Tính đạo hàm của hàm số tại Xo=0 bằng định nghĩa.
Có bao nhiêu điểm M thuộc đường cong (C):
y
x
+
1
x
-
1
sao cho tiếp tuyến của (C) tại M vuông góc với đường thẳng OM. A. 3. B. 2. C. 1. D. 4.
Đọc tiếp
Có bao nhiêu điểm M thuộc đường cong (C): y = x + 1 x - 1 sao cho tiếp tuyến của (C) tại M vuông góc với đường thẳng OM.
A. 3.
B. 2.
C. 1.
D. 4.
